HOME»基本情報技術者平成22年秋期問題»午後問8
基本情報技術者過去問題 平成22年秋期 午後問8
⇄問題文と設問を画面2分割で開く⇱問題PDF問8 データ構造及びアルゴリズム
次のプログラムの説明及びプログラムを読んで,設問1,2に答えよ。
プログラム1及びプログラム2は,いずれも二つの整数M,Nを受け取り,その積M×Nの値を返す。積は,加減算とシフト演算を使って求める。M,N及び求めた積は,いずれも符号付き2進数の整数で,負数は2の補数で表現する。
〔プログラム1の説明〕
プログラム1が受け取るM,Nは,いずれも4ビットで,各値の範囲は-8~7である。求めた積M×Nは,8ビットで返す。ただし,プログラム1中では,Mを5ビットに,Nを8ビットに拡張して処理を行う。
Rは13ビットの作業用変数であり,最下位から順にビット番号を0,1,… とし,最上位(符号ビット)のビット番号を12とする。Rは,指定した一部の範囲(例えば,ビット番号12~8の上位5ビット)だけを符号付き2進数とみなして部分的な算術演算ができる。また,値の検査のために指定したビット番号の内容を取り出すこともできる。
なお,⑥の行の加算では,けたあふれが起きても無視する。
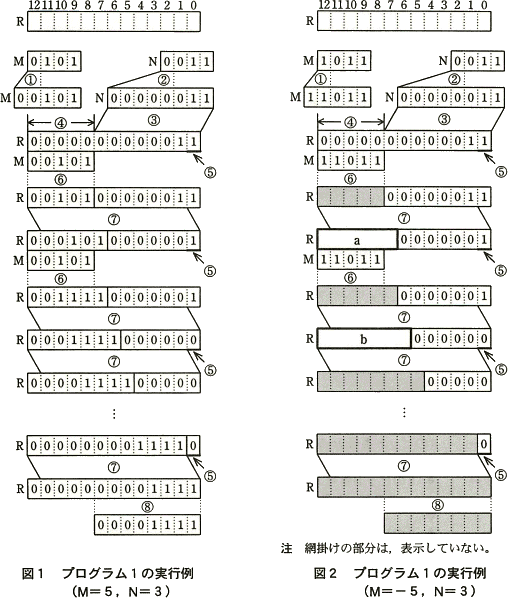
N=3として,M=5とM=-5の場合の処理過程を,それぞれ図1,2に示す。図1,2中の記号①~⑧は,プログラム1の①~⑧の行の処理と対応している。
 〔プログラム2の説明〕
〔プログラム2の説明〕
プログラム2が受け取るM,Nは,いずれも4ビットで,各値の範囲は -8~7である。求めた積M×Nは,8ビットで返す。ただし,プログラム2中では,Mを5ビットに拡張して処理を行う。
Rは10ビットの作業用変数であり,最下位から順にビット番号を0,1,… とし,最上位(符号ビット)のビット番号を9とする。Rは,指定した一部の範囲(例えば,ビット番号9~5の上位5ビット)だけを符号付き2進数とみなして部分的な算術演算ができる。また,値の検査のために指定したビット番号の内容を取り出すこともできる。
なお,⑤の行の加算及び⑦の行の減算では,けたあふれが起きても無視する。
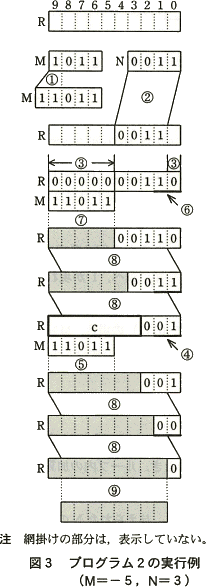
M=-5,N=3の場合の処理過程を図3に示す。図3中の記号①~⑨は,プログラム2の①~⑨の行の処理と対応している。
プログラム1及びプログラム2は,いずれも二つの整数M,Nを受け取り,その積M×Nの値を返す。積は,加減算とシフト演算を使って求める。M,N及び求めた積は,いずれも符号付き2進数の整数で,負数は2の補数で表現する。
〔プログラム1の説明〕
プログラム1が受け取るM,Nは,いずれも4ビットで,各値の範囲は-8~7である。求めた積M×Nは,8ビットで返す。ただし,プログラム1中では,Mを5ビットに,Nを8ビットに拡張して処理を行う。
Rは13ビットの作業用変数であり,最下位から順にビット番号を0,1,… とし,最上位(符号ビット)のビット番号を12とする。Rは,指定した一部の範囲(例えば,ビット番号12~8の上位5ビット)だけを符号付き2進数とみなして部分的な算術演算ができる。また,値の検査のために指定したビット番号の内容を取り出すこともできる。
なお,⑥の行の加算では,けたあふれが起きても無視する。
N=3として,M=5とM=-5の場合の処理過程を,それぞれ図1,2に示す。図1,2中の記号①~⑧は,プログラム1の①~⑧の行の処理と対応している。


プログラム2が受け取るM,Nは,いずれも4ビットで,各値の範囲は -8~7である。求めた積M×Nは,8ビットで返す。ただし,プログラム2中では,Mを5ビットに拡張して処理を行う。
Rは10ビットの作業用変数であり,最下位から順にビット番号を0,1,… とし,最上位(符号ビット)のビット番号を9とする。Rは,指定した一部の範囲(例えば,ビット番号9~5の上位5ビット)だけを符号付き2進数とみなして部分的な算術演算ができる。また,値の検査のために指定したビット番号の内容を取り出すこともできる。
なお,⑤の行の加算及び⑦の行の減算では,けたあふれが起きても無視する。
M=-5,N=3の場合の処理過程を図3に示す。図3中の記号①~⑨は,プログラム2の①~⑨の行の処理と対応している。


設問1
図2及び図3中の に入れる正しい答えを,解答群の中から選べ。
a に関する解答群
b,c に関する解答群
解答選択欄
- a:
- b:
- c:
解答
- a=エ
- b=オ
- c=イ
解説
このプログラムの流れを考える上でのポイントは、
〔a、bについて〕
アルゴリズムの流れを示す図2「プログラム1の実行例(M=-5、N=3)を参考に に入るビット列を考えていきます。
まず13ビットの作業領域Rを確保し、Mを符号付き5ビットに拡張、Nを符号付き8ビットに拡張します。
R=0000000000000
M=-5(10)→11011(2) //2の補数
N=3(10)→00000011(2)
次に、NをRの0~7番ビットに複写します。
R=0000000000011
ここからがループ処理です。
Rの0ビット目(最右ビット)が1なので、Rの8~12ビットにMを加算します。現在Rの8~12ビットは0で初期化されているので、2の補数で表現されたM(=-5)をそのまま複写します。
R=1101100000011
続く処理でRを右へ1ビット算術シフトした後の、7~12ビットがaの値となります。シフト前の符号ビット(最左ビット)は"1"なので、シフト後空となった12ビット目(最左ビット)には、符号と同じ"1"が入ります。
R=1110110000001
∴a=エ: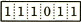
ループ2回目に移ります。
Rの0ビット目(最右ビット)が1なので、Rの8~12ビットにMを加算します。現在Rの8~12ビット"11101"は10進数では"-3"なので、M(=-5)を加算すると、
-3+(-5)=-8
-8を5ビットの2の補数で表すと、"11000"です。
したがって、加算後のRの8~12ビットには、10進数"-8"を2進数で表したビット列"11000"が入ることになります。
R=1100010000001
続く処理でRを右へ1ビット算術シフトした後の、7~12ビットが bの値となります。先程と同じように、Rを右へ1ビット算術シフトします。ここでも符号ビットは"1"なので、空いたビットには"1"が入ります。
R=1110001000000
∴b=オ: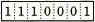
この後、Nのビット(現在のRの0~6ビット目)はすべて0なので、ループ内での処理は右へ1ビット算術シフトするだけとなります。
ループ6回分で右へび6ビットシフトさせると、
R=1111111110001
となり、Rの0~7ビット目の値がプログラムの返り値になります。
返却値=11110001
2進数11110001を、10進数に変換すると"-15"になるので、
M×N=(-5)×3=-15
の計算が正しく行われていることが確認できます。
〔cについて〕
アルゴリズムの流れを示す図3「プログラム2の実行例(M=-5、N=3)を参考に空欄に入るビット列を考えていきます。
プログラム1と異なる点に注意しながら流れを見ていきましょう。
まず10ビットの作業領域Rを確保し、Mを符号付き5ビットに拡張します。
R=0000000000
M=-5(10) → 11011(2) //2の補数
N=3(10) → 0011(2)
次に、NをRの1~4番ビットに複写します(※0からではなく、1からです)。
R=0000000110
ここからがループ処理です。ループ内では、Rの下位2ビットが"01"の時に加算処理、"10"の時に減算処理を行います。
現在のRの下位2ビットは"10"なので、M(=-5)をRの5~9ビット目から減算処理をします。現在Rの5~9ビットは0で初期化されているので、0-(-5)の計算を行い結果ビット列を複写します。
0-(-5)=5
計算結果の"5"は5ビットの2進数で"00101"なので、
R=0010100110
続いてR全体を右へ1ビット算術シフトします。プログラム1と同様に空いたビットには符号ビット同じ値が入ります。
R=0001010011
ループの2回目に移ります。現在のRの下位2ビットは"11"なので、加減算は行わずR全体を右へ1ビットシフトするだけです。シフト後のRの3~9ビット目がcのビット列になります。
R=0000101001
∴c=イ:
空欄に入るビット列はわかりましたが、最後までプログラムの流れを追っていくことにします。
ループ3回目、Rの下位2ビットは"01"なので、M(=-5)をRの5~9ビット目に加算処理をします。現在Rの5~9ビットは"00001"、10進数では"1"なので、1+(-5)の計算を行い結果ビット列を複写します。
1+(-5)=-4
計算結果の"-4"は5ビットの2の補数表現で"11100"なので、
R=1110001001
続いて、R全体を右へ1ビットシフトし、
R=1111000100
となります。
ループ4回目、Rの下位2ビットは"00"なので、加減算は行わずR全体を右へ1ビットシフトするだけです。
R=1111100010
ここまででループ処理は終了し、プログラムの返却値としてRの1~8ビット目が戻ることになります。
返却値=11110001
プログラム1と同様に11110001を、10進数に変換すると -15になるので、
M×N=(-5)×3=-15
の計算が正しく行われていることが確認できます。
以下にプログラムの実行例の空白部分を埋めた画像を掲載しておきますのでプログラム理解の参考にしてください。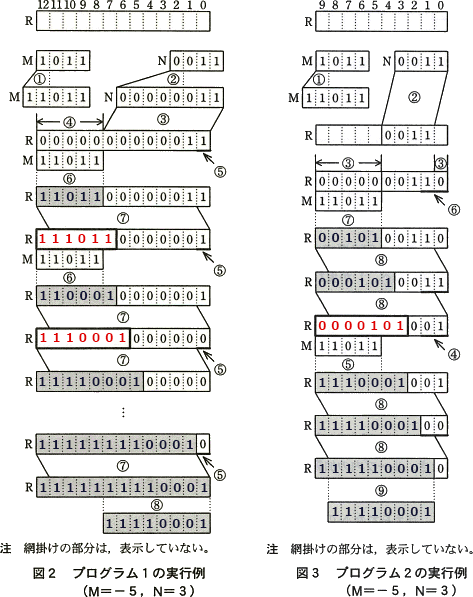
- 負数は2の補数で表現する。
- 算術シフトの時に時に空いたビットには符号と同じものが入る。
- 作業領域Rは、指定した一部の範囲をだけを符号付き2進数として部分的な算術計算ができる。
〔a、bについて〕
アルゴリズムの流れを示す図2「プログラム1の実行例(M=-5、N=3)を参考に に入るビット列を考えていきます。
まず13ビットの作業領域Rを確保し、Mを符号付き5ビットに拡張、Nを符号付き8ビットに拡張します。
R=0000000000000
M=-5(10)→11011(2) //2の補数
N=3(10)→00000011(2)
次に、NをRの0~7番ビットに複写します。
R=0000000000011
ここからがループ処理です。
Rの0ビット目(最右ビット)が1なので、Rの8~12ビットにMを加算します。現在Rの8~12ビットは0で初期化されているので、2の補数で表現されたM(=-5)をそのまま複写します。
R=1101100000011
続く処理でRを右へ1ビット算術シフトした後の、7~12ビットがaの値となります。シフト前の符号ビット(最左ビット)は"1"なので、シフト後空となった12ビット目(最左ビット)には、符号と同じ"1"が入ります。
R=1110110000001
∴a=エ:
ループ2回目に移ります。
Rの0ビット目(最右ビット)が1なので、Rの8~12ビットにMを加算します。現在Rの8~12ビット"11101"は10進数では"-3"なので、M(=-5)を加算すると、
-3+(-5)=-8
-8を5ビットの2の補数で表すと、"11000"です。
したがって、加算後のRの8~12ビットには、10進数"-8"を2進数で表したビット列"11000"が入ることになります。
R=1100010000001
続く処理でRを右へ1ビット算術シフトした後の、7~12ビットが bの値となります。先程と同じように、Rを右へ1ビット算術シフトします。ここでも符号ビットは"1"なので、空いたビットには"1"が入ります。
R=1110001000000
∴b=オ:
この後、Nのビット(現在のRの0~6ビット目)はすべて0なので、ループ内での処理は右へ1ビット算術シフトするだけとなります。
ループ6回分で右へび6ビットシフトさせると、
R=1111111110001
となり、Rの0~7ビット目の値がプログラムの返り値になります。
返却値=11110001
2進数11110001を、10進数に変換すると"-15"になるので、
M×N=(-5)×3=-15
の計算が正しく行われていることが確認できます。
〔cについて〕
アルゴリズムの流れを示す図3「プログラム2の実行例(M=-5、N=3)を参考に空欄に入るビット列を考えていきます。
プログラム1と異なる点に注意しながら流れを見ていきましょう。
まず10ビットの作業領域Rを確保し、Mを符号付き5ビットに拡張します。
R=0000000000
M=-5(10) → 11011(2) //2の補数
N=3(10) → 0011(2)
次に、NをRの1~4番ビットに複写します(※0からではなく、1からです)。
R=0000000110
ここからがループ処理です。ループ内では、Rの下位2ビットが"01"の時に加算処理、"10"の時に減算処理を行います。
現在のRの下位2ビットは"10"なので、M(=-5)をRの5~9ビット目から減算処理をします。現在Rの5~9ビットは0で初期化されているので、0-(-5)の計算を行い結果ビット列を複写します。
0-(-5)=5
計算結果の"5"は5ビットの2進数で"00101"なので、
R=0010100110
続いてR全体を右へ1ビット算術シフトします。プログラム1と同様に空いたビットには符号ビット同じ値が入ります。
R=0001010011
ループの2回目に移ります。現在のRの下位2ビットは"11"なので、加減算は行わずR全体を右へ1ビットシフトするだけです。シフト後のRの3~9ビット目がcのビット列になります。
R=0000101001
∴c=イ:
空欄に入るビット列はわかりましたが、最後までプログラムの流れを追っていくことにします。
ループ3回目、Rの下位2ビットは"01"なので、M(=-5)をRの5~9ビット目に加算処理をします。現在Rの5~9ビットは"00001"、10進数では"1"なので、1+(-5)の計算を行い結果ビット列を複写します。
1+(-5)=-4
計算結果の"-4"は5ビットの2の補数表現で"11100"なので、
R=1110001001
続いて、R全体を右へ1ビットシフトし、
R=1111000100
となります。
ループ4回目、Rの下位2ビットは"00"なので、加減算は行わずR全体を右へ1ビットシフトするだけです。
R=1111100010
ここまででループ処理は終了し、プログラムの返却値としてRの1~8ビット目が戻ることになります。
返却値=11110001
プログラム1と同様に11110001を、10進数に変換すると -15になるので、
M×N=(-5)×3=-15
の計算が正しく行われていることが確認できます。
以下にプログラムの実行例の空白部分を埋めた画像を掲載しておきますのでプログラム理解の参考にしてください。

設問2
次の記述中の に入れる正しい答えを,解答群の中から選べ。
- プログラム1の③の行では,積を求めるためのRの下位8ビットにNの値を設定している。それは,効率を考えてdためである。
- プログラム2はプログラム1と比べて,加減算の回数が少なくて済む場合がある。特に効果があるのはN<0のときで,このとき,プログラム1では,⑥の行の加算は最低でもe回実行されるが,プログラム2では,⑤の行の加算と⑦の行の減算との合計は最高でもf回で済む。
- プログラム1では,Nのビットが1の位置で加算をするので,例えばN=7(2進数で0111)なら,加算が3回必要である。一方,プログラム2では,Nの各ビットを最下位から順に調べ,1が現れたけた位置では減算をし,次に1の並びが途切れて0が現れたけた位置では加算をする,という処理を繰り返す。例えばN=7(2進数で0111)の場合,M×7をM×(g)として計算をするので,2進数での加減算の回数が2回で済む。
d に関する解答群
- 与えられたMの値が1のとき,ループ内の加算処理の実行回数を0にできる
- 与えられたNの値が1のとき,ループ内の加算処理の実行回数を0にできる
- 中間結果のシフトとNのビットの順次取出しを,1回のシフトで済ませる
- 中間結果のシフトによって,与えられたNの値の符号検査をなくせる
e,f に関する解答群
- 1
- 2
- 3
- 4
- 5
- 6
g に関する解答群
- -20+23
- -20+24
- -21+23
- -21+24
解答選択欄
- d:
- e:
- f:
- g:
解答
- d=ウ
- e=オ
- f=ウ
- g=ア
解説
〔dについて〕
〔eについて〕
プログラム1では、Nのビット列に1が少ないほど、⑥の加算処理の回数は少なくなります。Nの入力値(-8~7)のうち、N<0の4ビットの2進数で1のビットが最も少なくなるのは、10進数で-8、これを2の補数で表現した1000ですが、プログラム1ではその処理中でNを8ビットに拡張して処理をしています。
このため、Nも8ビットで表すことになり10進数"-8"は"11111000"となります。したがってN<0の時、⑥の加算処理の最低実行回数は5回ということになります。
∴e=オ:5
〔fについて〕
プログラム2で、加減算の回数が最も少なくなるN<0のときのビット列を考えます。
ループ中では作業領域Rの0,1ビット目が"01"または"10"のときに加減算を行いますので、ビット列が0から1に変わるとき、1から0に変わるときに演算が行われることになります。
プログラムの初期化部で、Rの0ビット目は0で初期化され、1~4ビット目にNが複写されるので、この5つのビットの組合せ中、最も0から1、1から0の切り替わりが多いものが演算回数が多くなるはずです。
N<0ではこの5ビットが"10100"、"10010"、"11010"、"10110"のときに演算回数が最も多く3回の演算が必要になります。
∴f=ウ:3
〔gについて〕
M×7=M×gとなるので、選択肢の式のなかで解が"7"になるものを見つければよいわけです。
- 誤り。ループ内の加算処理の実行回数が0になるのは、N=0の場合だけです。
- 誤り。N=1の時は、M×1という演算になります。Nの最下位ビットが1ですので1回の加算処理が実行されます。
- 正しい。
- 誤り。もともとプログラム中でNの符号検査はしていません。
〔eについて〕
プログラム1では、Nのビット列に1が少ないほど、⑥の加算処理の回数は少なくなります。Nの入力値(-8~7)のうち、N<0の4ビットの2進数で1のビットが最も少なくなるのは、10進数で-8、これを2の補数で表現した1000ですが、プログラム1ではその処理中でNを8ビットに拡張して処理をしています。
このため、Nも8ビットで表すことになり10進数"-8"は"11111000"となります。したがってN<0の時、⑥の加算処理の最低実行回数は5回ということになります。
∴e=オ:5
〔fについて〕
プログラム2で、加減算の回数が最も少なくなるN<0のときのビット列を考えます。
ループ中では作業領域Rの0,1ビット目が"01"または"10"のときに加減算を行いますので、ビット列が0から1に変わるとき、1から0に変わるときに演算が行われることになります。
プログラムの初期化部で、Rの0ビット目は0で初期化され、1~4ビット目にNが複写されるので、この5つのビットの組合せ中、最も0から1、1から0の切り替わりが多いものが演算回数が多くなるはずです。
N<0ではこの5ビットが"10100"、"10010"、"11010"、"10110"のときに演算回数が最も多く3回の演算が必要になります。
∴f=ウ:3
〔gについて〕
M×7=M×gとなるので、選択肢の式のなかで解が"7"になるものを見つければよいわけです。
- -20+23=-1+8=7
- -20+24=-1+16=15
- -21+23=-2+8=6
- -21+24=-2+16=14
