HOME»基本情報技術者平成27年春期問題»午後問8
基本情報技術者過去問題 平成27年春期 午後問8
⇄問題文と設問を画面2分割で開く⇱問題PDF問8 データ構造及びアルゴリズム
次のプログラムの説明及びプログラムを読んで,設問1~3に答えよ。
与えられたn個のデータの中からk番目に小さい値を選択する方法として,クイックソートを応用したアルゴリズムを考える。クイックソートとは,n個のデータをある基準値以下の値のグループと基準値以上の値のグループに分割し(基準値はどちらのグループに入れても構わない),更にそれぞれのグループで基準値を選んで二つのグループに分割するという処理を繰り返してデータを整列するアルゴリズムである。クイックソートを応用してk番目に小さい値を選択するアルゴリズムでは,データを二つのグループに分割した時点で,求める値はどちらのグループに含まれるかが確定するので,そのグループだけに,更に分割する処理を繰り返し適用する。グループの分割ができなくなった時点で,k番目に小さい値が選択されている。
〔プログラムの説明〕
n個の数値が格納されている配列xと値kを与えて,k番目に小さい値を返す関数 Select である。ここで,配列xの要素番号は1から始まる。また,配列xの大きさは,配列に格納される数値の個数分だけ確保されているものとする。Select の処理の流れを次に示す。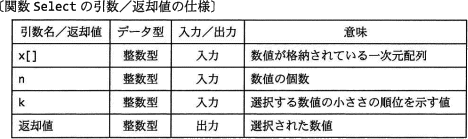

与えられたn個のデータの中からk番目に小さい値を選択する方法として,クイックソートを応用したアルゴリズムを考える。クイックソートとは,n個のデータをある基準値以下の値のグループと基準値以上の値のグループに分割し(基準値はどちらのグループに入れても構わない),更にそれぞれのグループで基準値を選んで二つのグループに分割するという処理を繰り返してデータを整列するアルゴリズムである。クイックソートを応用してk番目に小さい値を選択するアルゴリズムでは,データを二つのグループに分割した時点で,求める値はどちらのグループに含まれるかが確定するので,そのグループだけに,更に分割する処理を繰り返し適用する。グループの分割ができなくなった時点で,k番目に小さい値が選択されている。
〔プログラムの説明〕
n個の数値が格納されている配列xと値kを与えて,k番目に小さい値を返す関数 Select である。ここで,配列xの要素番号は1から始まる。また,配列xの大きさは,配列に格納される数値の個数分だけ確保されているものとする。Select の処理の流れを次に示す。
- 行番号3~4
k番目に小さい値を選択するために走査する範囲(以下,走査範囲という)の左端を Top,右端を Last とし,まず配列全体を走査範囲とする。 - 行番号5~32
- 走査範囲に含まれる要素の数が1以下になるまで,②,③を繰り返す。
- 基準値 Pivot を選び,走査範囲内の値で基準値以下のものを左に,基準値以上のものを右に集める(行番号6~24)。
- 走査範囲が基準値以下の値から成るグループと基準値以上の値から成るグループに分割されるので,k番目に小さい値が含まれるグループを新たな走査範囲とする(行番号25~30)。
- 繰返しが終了したときに,要素 x[k] の値がk番目に小さい値として,選択される。


設問1
関数 Select の追跡に関する次の記述中の に入れる正しい答えを,解答群の中から選べ。
関数 Select の引数で与えられた配列xの要素番号1~7の内容が3,5,6,4,7,2,1であり,nが7,kが3のとき,配列xの走査範囲の左端 Top と右端 Last の値は次のとおりに変化する。
関数 Select の引数で与えられた配列xの要素番号1~7の内容が3,5,6,4,7,2,1であり,nが7,kが3のとき,配列xの走査範囲の左端 Top と右端 Last の値は次のとおりに変化する。
- Top と Last の初期値は,それぞれ1と7である。
- Top<Last が成り立つ間,次に示す(1)選択処理1回目の①~③,(2)選択処理2回目の①~③,…と実行する。
- 選択処理1回目
- 配列xの走査範囲を二つの部分に分ける基準値 Pivot に配列xの3番目の要素x[3]の値 6 を設定する。次に,iに Top の値 1,jに Last の値 7 を設定する。
- 配列xの Top から Last までの走査範囲内にある数値を,6以下の数値のグループと6以上の数値のグループの二つに分ける処理を行う。その結果,配列xの内容は次のとおりになる。
3,5,1,4,2,7,6 - aを設定して選択処理の2回目に進む。
- 選択処理2回目
- 基準値 Pivot に x[3] の値 1 を設定する。
- 配列xの Top から Last までの走査範囲内にある数値を,1以下の数値のグループと1以上の数値のグループの二つに分ける処理を行う。その結果,配列xの内容は次のとおりになる。
1,5,3,4,2,7,6 - bを設定して選択処理の3回目に進む。
- 選択処理3回目
⋮
a,b に関する解答群
- Topに値1,Lastに値5
- Topに値1,Lastに値6
- Topに値2,Lastに値5
- Topに値2,Lastに値6
- Topに値3,Lastに値5
- Topに値3,Lastに値6
解答選択欄
- a:
- b:
解答
- a=ア
- b=ウ
解説
プログラムを見ると、Top=1、Last=nを初期値として、TopがLastより小さい間、以下の処理を繰り返しています。基本的な流れを確認しておきましょう。
配列xの要素は[3,5,6,4,7,2,1]で、k=3なので、1回目の選択処理では Pivot の値が x[3]=6 になります。
∴a=ア:Topに値1,Lastに値5
〔bについて〕
配列xの要素は[3,5,1,4,2,7,6]なので、2回目の選択処理では Pivot の値が x[3]=1 になります。
∴b=ウ:Topに値2,Lastに値5
- 10~12行目
- x[i] が Pivot 以上になるまで i を進めます。
- 13~15行目
- x[j] が Pivot 以下になるまで j を戻します。
- 16~18行目
- i が j 以上ならばループを抜け、25~30行目のTopとLastを再設定する処理に移ります。
- 19~23行目
- x[i] と x[j] を交換します。その後、iに1を足し、jから1を引きます。
- 15~30行目
- iがk以下ならば探索範囲の先頭を j+1 に変更し、jがk以上ならば探索範囲の末尾を i-1 に変更します。
配列xの要素は[3,5,6,4,7,2,1]で、k=3なので、1回目の選択処理では Pivot の値が x[3]=6 になります。
- iが1から3まで進み、jは7のままです。
3,5,6(i),4,7,2,1(j) - x[i] と x[j] を交換(赤字部分)し、i+1、j-1を行うと、以下のようになります。
3,5,1,4(i),7,2(j),6 - iが7の位置まで進み、jは6の位置のままです。
3,5,1,4,7(i),2(j),6 - x[i] と x[j] を交換し、i+1、j-1を行うと、以下のようになります。
3,5,1,4,2(j),7(i),6 - x[i]≧6、x[j]≦6なので、iとjはどちらも移動しません。
- i≧j となったのでbreak文でループを抜けます。この時点で、i=6、j=5です。
- i>3 なのでTopは1のまま、j≧3 なのでLastには i-1、すなわち「6-1=5」が格納されます。
∴a=ア:Topに値1,Lastに値5
〔bについて〕
配列xの要素は[3,5,1,4,2,7,6]なので、2回目の選択処理では Pivot の値が x[3]=1 になります。
- iは1のまま、jは5から3まで戻ります。
3(i),5,1(j),4,2,7,6 - x[i] と x[j] を交換し、i+1、j-1を行うと、以下のようになります。
1,5(i,j),3,4,2,7,6 - iは2のまま、jは1まで戻ります。
1(j),5(i),3,4,2,7,6 - i≧j となったのでbreak文でループを抜けます。この時点で、i=2、j=1です。
- i≦3 なのでTopには j+1、すなわち「1+1=2」が格納されます。j<3 なのでLastは5のままです。
∴b=ウ:Topに値2,Lastに値5
設問2
次の記述中の に入れる正しい答えを,解答群の中から選べ。
引数で与えられた配列xの要素番号1~7の内容が1,3,2,4,2,2,2であり,nが 7,kが 3 のとき,選択処理が終了するまでにプログラム中のαの部分はc回実行され,γの部分はd回実行される。
引数で与えられた配列xの要素番号1~7の内容が1,3,2,4,2,2,2であり,nが 7,kが 3 のとき,選択処理が終了するまでにプログラム中のαの部分はc回実行され,γの部分はd回実行される。
c,d に関する解答群
- 1
- 2
- 3
- 4
- 5
- 6
解答選択欄
- c:
- d:
解答
- c=イ
- d=エ
解説
〔cdについて〕
配列xの要素は[1,3,2,4,2,2,2]で、k=3なので、1回目の選択処理では Pivot の値が x[3]=2 になります。設問1と同じように処理をトレースしていきます。
αの処理は選択処理を行った回数だけ実行されるので2回、γの処理は配列要素の交換を行った回数だけ実行されるので4回となります。
∴c=イ:2
d=エ:4
配列xの要素は[1,3,2,4,2,2,2]で、k=3なので、1回目の選択処理では Pivot の値が x[3]=2 になります。設問1と同じように処理をトレースしていきます。
- Topに1を、Lastに7を設定します(α)。
- iが1から2まで進み、jは7のままです。
1,3(i),2,4,2,2,2(j) - x[i] と x[j] を交換し、i+1、j-1を行うと、以下のようになります。
1,2,2(i),4,2,2(j),3 - iとjともに変化せずそのままの位置です。
1,2,2(i),4,2,2(j),3 - x[i] と x[j] を交換し、i+1、j-1を行うと、以下のようになります。
1,2,2,4(i),2(j),2,3 - iとjともに変化せずそのままの位置です。
1,2,2,4(i),2(j),2,3 - x[i] と x[j] を交換し、i+1、j-1を行うと、以下のようになります。
1,2,2,2(j),4(i),2,3 - x[i]≧2、x[j]≦2なので、iとjともに移動せずそのままの位置です。
- i≧j となったのでbreak文でループを抜けます。この時点で、i=5、j=4です。
- i>3 なのでTopは1のまま、j≧3 なのでLastには i-1、すなわち「5-1=4」が格納されます。
- Topに1を、Lastに4を設定します(α)。
- iが1から2まで進み、jは4のままです。
1,2(i),2,2(j),4,2,3 - x[i] と x[j] を交換し、i+1、j-1を行うと、以下のようになります。
1,2,2(i,j),2,4,2,3 - x[i]≧2、x[j]≦2なので、iとjともに移動せずそのままの位置です。
- i≧jとなったのでbreak文でループを抜けます。この時点で、i=3、j=3です。
- i≦3 なのでTopなのでTopには j+1、すなわち「3+1=4」が格納されます。j≧3なのでLastには i-1、すなわち「3-1=2」が格納されます。
αの処理は選択処理を行った回数だけ実行されるので2回、γの処理は配列要素の交換を行った回数だけ実行されるので4回となります。
∴c=イ:2
d=エ:4
設問3
次の記述中の に入れる正しい答えを,解答群の中から選べ。
プログラム中のβの行 x[i]<Pivot を誤って x[i]≦Pivot とした。この場合,引数で与えられた配列xの要素番号1~6の内容が1,1,1,1,1,1であり,nが 6,kが 3 のときe。また,引数で与えられた配列xの要素番号1~6の内容が1,3,2,4,2,2であり,n が6,k が3のとき,f。
プログラム中のβの行 x[i]<Pivot を誤って x[i]≦Pivot とした。この場合,引数で与えられた配列xの要素番号1~6の内容が1,1,1,1,1,1であり,nが 6,kが 3 のときe。また,引数で与えられた配列xの要素番号1~6の内容が1,3,2,4,2,2であり,n が6,k が3のとき,f。
e,f に関する解答群
- Lastに値 0 が設定される
- Pivotに値 0 が設定される
- Topに値 0 が設定される
- 処理が終了しない
- 配列の範囲を越えて参照する
解答選択欄
- e:
- f:
解答
- e=オ
- f=エ
解説
〔eについて〕
x[i]≦Pivot とすると配列要素の値がPivotを超えるまで i が進むことになります。配列要素が[1,1,1,1,1,1]、Pivotが1の場合、iは配列要素の末尾(n)を越えて増加し、定義外の要素である x[7] を参照することになります。これにより参照エラーを起こします。
∴e=オ:配列の範囲を越えて参照する
〔fについて〕
配列要素が[1,3,2,4,2,2]の場合、次のように処理が進みます。
選択処理1回目の Pivot は x[2]=2 です。
∴f=エ:処理が終了しない
x[i]≦Pivot とすると配列要素の値がPivotを超えるまで i が進むことになります。配列要素が[1,1,1,1,1,1]、Pivotが1の場合、iは配列要素の末尾(n)を越えて増加し、定義外の要素である x[7] を参照することになります。これにより参照エラーを起こします。
∴e=オ:配列の範囲を越えて参照する
〔fについて〕
配列要素が[1,3,2,4,2,2]の場合、次のように処理が進みます。
選択処理1回目の Pivot は x[2]=2 です。
- Topに1を、Lastに6を設定します。
- iが1から2の位置まで進み、jは6のままです。
1,3(i),2,4,2,2(j) - x[i] と x[j] を交換(赤字部分)し、i+1、j-1を行うと、以下のようになります。
1,2,2(i),4,2(j),3 - iが4の位置まで進み、jは5のままです。
1,2,2,4(i),2(j),3 - x[i] と x[j] を交換(赤字部分)し、i+1、j-1を行うと、以下のようになります。
1,2,2,2(j),4(i),3 - x[i]≧2、x[j]≦2なので、iとjともに移動せずそのままの位置です。
- i≧j となったのでbreak文でループを抜けます。この時点で、i=5、j=4です。
- i>3 なのでTopは1のまま、j≧3なのでLastには i-1、すなわち「5-1=4」が格納されます。
- Topに1を、Lastに4を設定します。
- iが1から5の位置まで進み、jは4のままです。
1,2,2,2(j),4(i),3 - x[i]≧2、x[j]≦2なので、iとjともに移動せずそのままの位置です。
- i≧j となったのでbreak文でループを抜けます。この時点で、i=5、j=4です。
- i>3 なのでTopは1のまま、j≧3 なのでLastには i-1、すなわち「5-1=4」が格納されます。
∴f=エ:処理が終了しない
