HOME»基本情報技術者平成29年秋期問題»午後問4
基本情報技術者過去問題 平成29年秋期 午後問4
⇄問題文と設問を画面2分割で開く⇱問題PDF問4 ネットワーク
コールセンタ設備の構成案及び必要となるオペレータ数の検討に関する次の記述を読んで,設問1,2に答えよ。
X社のコールセンタでは,顧客からの問合せの電話に対して30人のオペレータで処理を行っているが,"電話で待たされる"という顧客からの意見が多く寄せられている。この度,顧客が電話で待たされる時間の短縮を目的に,既存のコールセンタの設備とオペレータ数を見直すことにした。検討の要件とコールセンタ設備の構成案は,次のとおりである。
〔検討の要件〕
〔コールセンタ設備の構成案〕
VoIPサーバ群は,顧客情報サーバ,コールサーバ及び着信分配情報サーバで構成する。オペレータ席には,それぞれ電話端末とPCを設置する。VoIPサーバ群と,音声ゲートウェイ及びオペレータ席との間はレイヤ3スイッチで接続する。
コールセンタ設備の構成案を,図1に示す。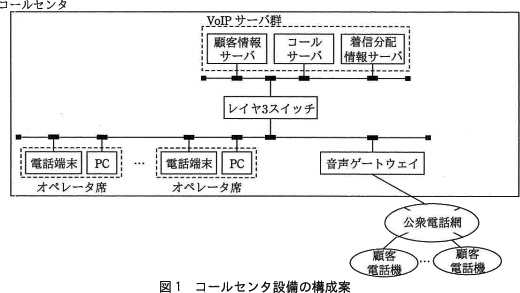 顧客情報サーバは,過去の問合せ内容の検索や,顧客とのやり取りを記録するために利用される。コールサーバはVoIPの制御を行い,音声ゲートウェイから電話の接続要求があると,オペレータ席にある電話端末とPCの状態(以下,オペレータ席の状態という)を管理している着信分配情報サーバに問い合わせて,接続要求待ちのオペレータ席の電話端末へ接続する。オペレータ席の状態には,接続要求待ち,通話中及び結果記録中の状態があり,着信分配情報サーバは各オペレータ席がどの状態にあるかを認識している。
顧客情報サーバは,過去の問合せ内容の検索や,顧客とのやり取りを記録するために利用される。コールサーバはVoIPの制御を行い,音声ゲートウェイから電話の接続要求があると,オペレータ席にある電話端末とPCの状態(以下,オペレータ席の状態という)を管理している着信分配情報サーバに問い合わせて,接続要求待ちのオペレータ席の電話端末へ接続する。オペレータ席の状態には,接続要求待ち,通話中及び結果記録中の状態があり,着信分配情報サーバは各オペレータ席がどの状態にあるかを認識している。
顧客からの通話要求をオペレータ席の電話端末に接続するシーケンスを,図2に示す。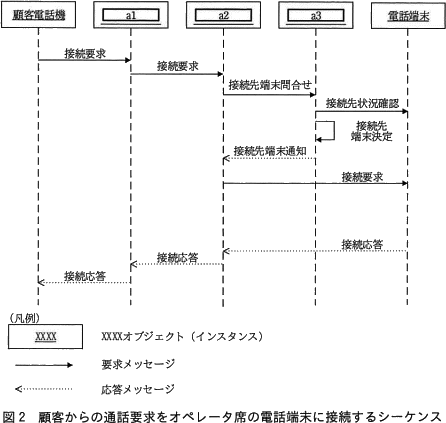
X社のコールセンタでは,顧客からの問合せの電話に対して30人のオペレータで処理を行っているが,"電話で待たされる"という顧客からの意見が多く寄せられている。この度,顧客が電話で待たされる時間の短縮を目的に,既存のコールセンタの設備とオペレータ数を見直すことにした。検討の要件とコールセンタ設備の構成案は,次のとおりである。
〔検討の要件〕
- コールセンタでは,IPをベースにして拡張が可能なVoIP(Voice over Internet Protocol)を採用する。
- コールセンタに着信があってからオペレータと通話を開始できるまでの平均待ち時間を,問合せが最も多い時間帯(以下,ピーク時という)においても,20秒以下になるようにオペレータを増員する。
〔コールセンタ設備の構成案〕
VoIPサーバ群は,顧客情報サーバ,コールサーバ及び着信分配情報サーバで構成する。オペレータ席には,それぞれ電話端末とPCを設置する。VoIPサーバ群と,音声ゲートウェイ及びオペレータ席との間はレイヤ3スイッチで接続する。
コールセンタ設備の構成案を,図1に示す。

顧客からの通話要求をオペレータ席の電話端末に接続するシーケンスを,図2に示す。

設問1
図2中の に入れる正しい答えを,解答群の中から選べ。ここで,a1~a3に入れる答えは,aに関する解答群の中から組合せとして正しいものを選ぶものとする。
a に関する解答群

解答選択欄
- a:
解答
- a=イ
解説
VoIP(Voice over IP:ボイップ)は、音声データをIPネットワークで伝送する技術です。アナログ音声を各種符号化方式でデジタル化し、IPネットワーク上のパケットに乗せることで音声データのリアルタイム伝送を行います。
〔aについて〕
問題文中の〔コールセンタ設備の構成案〕には各サーバの役割が説明されています。 図2のシーケンス図を見ると、電話端末に対して接続状況を確認し、接続先を決定しているa3が着信分配サーバとわかります。さらに着信分配サーバに問合せを行っているa2はコールサーバになります。そして顧客電話機からの接続要求を受け、コールサーバに接続要求を行っているa1が音声ゲートウェイです。
図2のシーケンス図を見ると、電話端末に対して接続状況を確認し、接続先を決定しているa3が着信分配サーバとわかります。さらに着信分配サーバに問合せを行っているa2はコールサーバになります。そして顧客電話機からの接続要求を受け、コールサーバに接続要求を行っているa1が音声ゲートウェイです。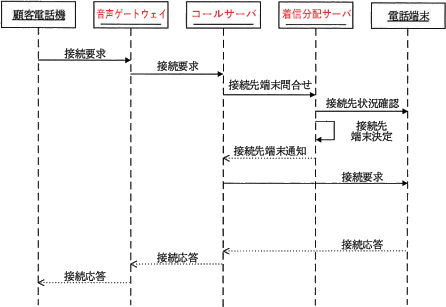 したがって「イ」の組合せが適切です。
したがって「イ」の組合せが適切です。
〔aについて〕
問題文中の〔コールセンタ設備の構成案〕には各サーバの役割が説明されています。
- 顧客情報サーバ
- 過去の問合せ情報の検索や,顧客との役割を記録するために利用される。
- コールサーバ
- 音声ゲートウェイから電話の接続要求があると,…着信分配サーバに問い合わせて,接続要求待ちの電話端末に接続する
- 着信分配サーバ
- 各オペレータ席がどの状態にあるかを認識している。

設問2
次の記述中の に入れる正しい答えを,解答群の中から選べ。
〔オペレータ席の状態と問合せの処理件数及び処理時間〕
接続要求待ちの状態にあるオペレータ席の電話端末に接続要求があると,オペレータが顧客と通話を開始することによって通話中の状態になる。通話が終了すると結果記録中の状態となり,オペレータはPCから顧客情報サーバに,その結果の記録を行う。結果の記録が完了すると,接続要求待ちの状態に戻る。
X社のコールセンタが想定する問合せの処理件数及び平均処理時間を表1に示す。1人のオペレータが1回の問合せに応対する通話時間と,結果記録時間の合計を処理時間とする。想定する平均処理時間はb分であり,コールセンタのピーク時における平均着信間隔はc秒となる。 〔必要なオペレータ数の検討〕
〔必要なオペレータ数の検討〕
コールセンタに顧客からの着信があってから,オペレータと通話を開始できるまでの平均待ち時間の算出には,待ち行列理論を使う。窓口数sの M/M/s モデルに表1の条件を適用すると,オペレータ数と平均待ち行列長の関係は,表2のようになることが分かっている。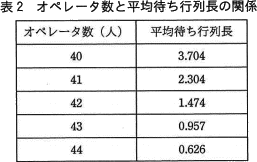 平均到着率(平均着信間隔の逆数)をλとすると,平均待ち行列長Lと平均待ち時間Wとの間には,次のリトルの公式が成立する。
平均到着率(平均着信間隔の逆数)をλとすると,平均待ち行列長Lと平均待ち時間Wとの間には,次のリトルの公式が成立する。
〔オペレータ席の状態と問合せの処理件数及び処理時間〕
接続要求待ちの状態にあるオペレータ席の電話端末に接続要求があると,オペレータが顧客と通話を開始することによって通話中の状態になる。通話が終了すると結果記録中の状態となり,オペレータはPCから顧客情報サーバに,その結果の記録を行う。結果の記録が完了すると,接続要求待ちの状態に戻る。
X社のコールセンタが想定する問合せの処理件数及び平均処理時間を表1に示す。1人のオペレータが1回の問合せに応対する通話時間と,結果記録時間の合計を処理時間とする。想定する平均処理時間はb分であり,コールセンタのピーク時における平均着信間隔はc秒となる。

コールセンタに顧客からの着信があってから,オペレータと通話を開始できるまでの平均待ち時間の算出には,待ち行列理論を使う。窓口数sの M/M/s モデルに表1の条件を適用すると,オペレータ数と平均待ち行列長の関係は,表2のようになることが分かっている。

λ×W=L
リトルの公式と表2を用いると,ピーク時の平均待ち時間を20秒以下にするために必要なオペレータ数は最少d人となる。ここで,接続要求待ちの状態にあるオペレータ席が一つ以上ある場合に,コールセンタに顧客からの着信があってからオペレータ席の電話端末に接続要求を行うまでの時間と,オペレータが接続応答を行ってから顧客と通話を開始できるまでの時間は,無視できるほど短いものとする。b,c に関する解答群
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
d に関する解答群
- 40
- 41
- 42
- 43
- 44
解答選択欄
- b:
- c:
- d:
解答
- b=エ
- c=ク
- d=ウ
解説
〔bについて〕
処理時間は、「1回の問合せに応対する通話時間と,結果記録時間の合計」です。表1より、平均通話時間は4分/件、平均結果記録時間は2分/件と分かるので、平均処理時間は2つを足し合わせた6分です。
∴b=エ:6
〔cについて〕
表1よりピーク時には1時間当たり360件の着信があると分かります。1時間は3,600秒ですから、平均着信間隔は、
3,600÷360=10(秒)
平均すれば10秒に1件の着信があることになります。
∴c=ク:10
〔dについて〕
問題文中に示されているリトルの公式「λ×W=L」を利用して答えを求めます。
平均着信間隔は10秒なので、平均到着率(λ)はその逆数である1/10になります。そして平均待ち時間(W)は目標値の20秒を使用します。
リトルの公式にλ(1/10)、W(20)を代入すると、この条件下における平均待ち行列長(L)を求められます。
1/10×20=L
2=L
このLは、平均待ち時間が20秒であるときの平均待ち行列長を示します。平均待ち行列長が長くなるほど平均待ち時間も増加するので、目標達成のためにはピーク時におけるLを2以下に抑えなければなりません。表2「オペレータ数と平均待ち行列長の関係」を見ると、平均待ち行列長が2以下となるのはオペレータ数が42人以上の場合です。すなわち目標達成のために必要な最少のオペレータ数は42人になります。
∴d=ウ:42
処理時間は、「1回の問合せに応対する通話時間と,結果記録時間の合計」です。表1より、平均通話時間は4分/件、平均結果記録時間は2分/件と分かるので、平均処理時間は2つを足し合わせた6分です。
∴b=エ:6
〔cについて〕
表1よりピーク時には1時間当たり360件の着信があると分かります。1時間は3,600秒ですから、平均着信間隔は、
3,600÷360=10(秒)
平均すれば10秒に1件の着信があることになります。
∴c=ク:10
〔dについて〕
問題文中に示されているリトルの公式「λ×W=L」を利用して答えを求めます。
平均着信間隔は10秒なので、平均到着率(λ)はその逆数である1/10になります。そして平均待ち時間(W)は目標値の20秒を使用します。
リトルの公式にλ(1/10)、W(20)を代入すると、この条件下における平均待ち行列長(L)を求められます。
1/10×20=L
2=L
このLは、平均待ち時間が20秒であるときの平均待ち行列長を示します。平均待ち行列長が長くなるほど平均待ち時間も増加するので、目標達成のためにはピーク時におけるLを2以下に抑えなければなりません。表2「オペレータ数と平均待ち行列長の関係」を見ると、平均待ち行列長が2以下となるのはオペレータ数が42人以上の場合です。すなわち目標達成のために必要な最少のオペレータ数は42人になります。
∴d=ウ:42
