HOME»基本情報技術者令和元年秋期問題»午後問13
基本情報技術者過去問題 令和元年秋期 午後問13
⇄問題文と設問を画面2分割で開く⇱問題PDF⇱表計算ソフトの機能・用語問13 ソフトウェア開発(表計算)
次の表計算のワークシート及びマクロの説明を読んで,設問1,2に答えよ。
Z組合では,収穫したメロンのうち1kg以上かつ3kg未満のものだけを組合で決めた3等級に分類して直接小売店に出荷している。出荷するメロンの等級と価格を決定する処理に,表計算ソフトを用いている。
〔メロンの等級〕
出荷するメロンは,形状及び表皮色をそれぞれ評価して"優","良","並"のいずれかに分類する。評価は"優"が最も高く,"並"が最も低い。形状と表皮色の評価のうち低い方が,そのメロンの等級となる。メロンの等級ごとに"キログラム当たり単価"が設定されている。
〔ワークシート:単価表〕
キログラム当たり単価が格納されたワークシート"単価表"を,図1に示す。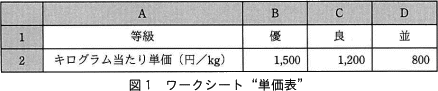
1回の出荷ごとに,出荷する個々のメロンに対して一意となるIDを付与する。1回の出荷数は1,000個以内である。各メロンの等級と価格(価格は,等級が"優"と"良"のものだけ)を決定するワークシート"集計表"の例を,図2に示す。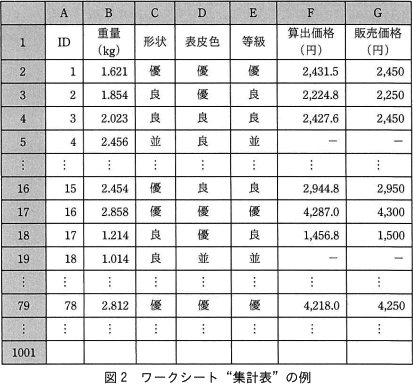
Z組合では,収穫したメロンのうち1kg以上かつ3kg未満のものだけを組合で決めた3等級に分類して直接小売店に出荷している。出荷するメロンの等級と価格を決定する処理に,表計算ソフトを用いている。
〔メロンの等級〕
出荷するメロンは,形状及び表皮色をそれぞれ評価して"優","良","並"のいずれかに分類する。評価は"優"が最も高く,"並"が最も低い。形状と表皮色の評価のうち低い方が,そのメロンの等級となる。メロンの等級ごとに"キログラム当たり単価"が設定されている。
〔ワークシート:単価表〕
キログラム当たり単価が格納されたワークシート"単価表"を,図1に示す。

- 列Aは,見出し列である。
- セル B1~D1 には,等級として,順に"優","良","並"を入力する。
- セル B2~D2 には,各等級のキログラム当たり単価を入力する。
1回の出荷ごとに,出荷する個々のメロンに対して一意となるIDを付与する。1回の出荷数は1,000個以内である。各メロンの等級と価格(価格は,等級が"優"と"良"のものだけ)を決定するワークシート"集計表"の例を,図2に示す。

- 行1は見出し行である。出荷するメロンのデータは,行2以降にそれぞれ1行で入力する。
- データの最終行よりも下の行の列A~Dの各セルには空値が入力されている。
- 列Aには,付与したIDを入力する。
- 列Bには,メロンの重量をkg単位で小数第3位まで入力する。
- 列Cと列Dには,メロンの形状と表皮色の評価をそれぞれ入力する。
- セル E2 には,セル C2 及び D2 の評価に基づいて,メロンの等級を表示する次の式を入力し,セル E3~E1001 に複写する。
IF(A2=null,null,a) - セル F2 には,次の式を入力し,セル F3~F1001 に複写する。この式は,等級が"並"のときは"-"を表示し,それ以外のときは,メロンの算出価格を表示する。算出価格は,ワークシート"単価表"を参照して,メロンのキログラム当たり単価に重量を掛けた値である。
IF(A2=null,null,IF(E2='並',"-",b*B2)) - セル G2 には,次の式を入力し,セル G3~G1001に複写する。この式は,等級が"並"のときは"-"を表示し,それ以外のときは,メロンの販売価格を表示する。販売価格は,算出価格を50円単位で切り上げた値である。
IF(A2=null,null,IF(E2='並','-',c))
設問1
ワークシート"集計表"の説明文中の に入れる正しい答えを,解答群の中から選べ。
a に関する解答群
- IF(論理積(C2='並',D2='並'),'並',
IF(論理積(C2='良',D2='良'),'良','優')) - IF(論理積(C2='優',D2='優'),'優',
IF(論理積(C2='並',D2='並'),'並','良')) - IF(論理積(C2='優',D2='優'),'優',
IF(論理積(C2='良',D2='良'),'良','並')) - IF(論理和(C2='並',D2='並'),'並',
IF(論理和(C2='良',D2='良'),'良','優')) - IF(論理和(C2='優',D2='優'),'優',
IF(論理和(C2='並',D2='並'),'並','良')) - IF(論理和(C2='優',D2='優'),'優',
IF(論理和(C2='良',D2='良'),'良','並'))
b に関する解答群
- 照合一致(E2,単価表!$B2:$D2,0)
- 照合一致(E2,単価表!B$2:D$2,0)
- 水平照合(E2,単価表!$B1:$D2,2,0)
- 水平照合(E2,単価表!B$1:D$2,2,0)
- 表引き(単価表!$B1:$D2,2,1)
- 表引き(単価表!B$1:D$2,2,1)
c に関する解答群
- 切上げ(F2*2,0)/2
- 切上げ(F2/2,0)*2
- 切上げ(F2/50,0)*50
- 四捨五入(F2,-2)
- 四捨五入(F2+50,-2)-50
- 四捨五入(F2/50,0)*50
解答選択欄
- a:
- b:
- c:
解答
- a=エ
- b=エ
- c=ウ
解説
〔aについて〕
IF文を使用してメロンの等級を表示させる式が入ります。
メロンの等級は、「形状と表皮色の評価の低い方」になります。表にしてみると次の通りです。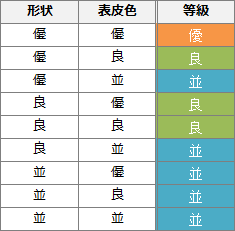 形状と表皮色のいずれか一方が"並"であれば等級は"並"、それ以外の場合でいずれか一方が"良"であれば等級は"良"と判定されます。これをIF文で実現します。
形状と表皮色のいずれか一方が"並"であれば等級は"並"、それ以外の場合でいずれか一方が"良"であれば等級は"良"と判定されます。これをIF文で実現します。
形状の値はセル C2 に、表皮色の値はセル D2 に格納されているので、いずれか一方が"並"のときに真となる条件式は、
この式が真となるときには"並"を表示するので、
どちらの値も"並"でない場合は、さらにIF文を入れ子構造にして"良"と"優"の出力を分けます。いずれか一方が"良"のときには"良"を表示し、それ以外のとき(両方とも"優")には"優"を表示したいので、条件式が真となる場合には"良"、偽の場合には"優"を返す以下の式が適切です。
∴a=エ
〔bについて〕
等級が"優"または"良"であるときに、単価表から対応する単価を取得する式が入ります。
まず、各式の絶対参照の位置を見てみましょう。bを含む式はセル F3~F1001 に複写されますが、単価表のセル範囲は複写先のセルにおいても常に同一の行を参照するようになっていなければなりません。この点から言えば、行指定に絶対参照($)が付されていない「ア」「ウ」「オ」は誤りであると判断できます。
「イ」の照合一致は、単価表 B2~D2 の1行から等級の値(E2)が一致するセルを探し、そのセル範囲の中での相対位置を返します。単価の行を等級の値で探索することになるので一致することはありません。また、そもそも照合一致は相対位置を返す関数です。セルの値を返さないので単価を取得することはできません。
「エ」の水平照合は、単価表 B1~D2 の上端行である B1~D1 を左から右に走査して、第1引数で指定された等級の値を探します。一致するセルが見つかると、その列の上端行から数えて2行目の値を返します。等級の値が"優"であれば2行目の"1,500"を、等級の値が"良"であれば2行目の"1,200"を返すため適切な式です。よって「エ」が正解です。 「カ」の表引きは、単価表 B1~D2 のセル範囲の左上から数えて、行2列1の位置にあるセルの値を返します。この式では等級の値によらず常にB2の値である"1,500"を返すため誤りです。
「カ」の表引きは、単価表 B1~D2 のセル範囲の左上から数えて、行2列1の位置にあるセルの値を返します。この式では等級の値によらず常にB2の値である"1,500"を返すため誤りです。 ∴b=エ
∴b=エ
〔cについて〕
"切上げ"と"四捨五入"は、第1引数の値を第2引数で指定された位で概数に変換する関数です。第2引数は小数第1位の桁を0とし、右の桁であるほど数が増え、左の桁であるほど数が減ります。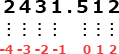 〔ワークシート:"集計表"〕(8)に「販売価格は,算出価格を50円単位で切り上げた値」であると説明されているため、使用する関数は"切上げ"です。ここでは、重量集計表のセル F2 の値である2431.5が、式を通した後にセル G2 の2,450に正しく変換されるかどうかを確認することで適切な式を導きます。
〔ワークシート:"集計表"〕(8)に「販売価格は,算出価格を50円単位で切り上げた値」であると説明されているため、使用する関数は"切上げ"です。ここでは、重量集計表のセル F2 の値である2431.5が、式を通した後にセル G2 の2,450に正しく変換されるかどうかを確認することで適切な式を導きます。
∴c=ウ
IF文を使用してメロンの等級を表示させる式が入ります。
メロンの等級は、「形状と表皮色の評価の低い方」になります。表にしてみると次の通りです。

形状の値はセル C2 に、表皮色の値はセル D2 に格納されているので、いずれか一方が"並"のときに真となる条件式は、
論理和(C2='並', D2='並')
となります。この式が真となるときには"並"を表示するので、
IF(論理和(C2='並', D2='並'), '並', …)
までが確定します。どちらの値も"並"でない場合は、さらにIF文を入れ子構造にして"良"と"優"の出力を分けます。いずれか一方が"良"のときには"良"を表示し、それ以外のとき(両方とも"優")には"優"を表示したいので、条件式が真となる場合には"良"、偽の場合には"優"を返す以下の式が適切です。
IF(論理和(C2='良', D2='良'), '良', '優')
したがって、上記の2つを組み合わせた次の式が正解となります。IF(論理和(C2='並', D2='並'), '並',
IF(論理和(C2='良', D2='良'), '良', '優'))
「ア」「イ」は両方が"並"の場合にしか"並"を返さないため、「ウ」は両方が"良"の場合にしか"良"を返さないため、「オ」「カ」は一方が"優"であれば"優"を返すため誤りです。IF(論理和(C2='良', D2='良'), '良', '優'))
∴a=エ
〔bについて〕
等級が"優"または"良"であるときに、単価表から対応する単価を取得する式が入ります。
まず、各式の絶対参照の位置を見てみましょう。bを含む式はセル F3~F1001 に複写されますが、単価表のセル範囲は複写先のセルにおいても常に同一の行を参照するようになっていなければなりません。この点から言えば、行指定に絶対参照($)が付されていない「ア」「ウ」「オ」は誤りであると判断できます。
「イ」の照合一致は、単価表 B2~D2 の1行から等級の値(E2)が一致するセルを探し、そのセル範囲の中での相対位置を返します。単価の行を等級の値で探索することになるので一致することはありません。また、そもそも照合一致は相対位置を返す関数です。セルの値を返さないので単価を取得することはできません。
「エ」の水平照合は、単価表 B1~D2 の上端行である B1~D1 を左から右に走査して、第1引数で指定された等級の値を探します。一致するセルが見つかると、その列の上端行から数えて2行目の値を返します。等級の値が"優"であれば2行目の"1,500"を、等級の値が"良"であれば2行目の"1,200"を返すため適切な式です。よって「エ」が正解です。


〔cについて〕
"切上げ"と"四捨五入"は、第1引数の値を第2引数で指定された位で概数に変換する関数です。第2引数は小数第1位の桁を0とし、右の桁であるほど数が増え、左の桁であるほど数が減ります。
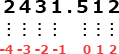
- 2431.5×2=4863
4863を小数第1位で切上げ→4863
4863÷2=2431.5(×) - 2431.5÷2=1215.75
1215.75を小数第1位で切上げ→1216
1216×2=2432(×) - 2431.5÷50=48.63
48.63を小数第1位で切上げ→49
49×50=2450(〇)
∴c=ウ
設問2
等級が"優"及び"良"のメロンは,1個ずつ箱に入れて梱包する。等級が"並"のメロンは,複数個を大箱に入れて梱包する。大箱の販売価格は,梱包したメロンの合計重量に,等級が"並"のキログラム当たり単価を掛けて,50円単位で切り上げた値である。等級が"並"のメロンを大箱に割り振るために,ワークシート"重量計算表"を作成し,マクロ Packing を格納した。マクロ Packing 中の に入れる正しい答えを,解答群の中から選べ。
〔ワークシート:重量計算表〕
ワークシート"集計表"の行2以降のデータを上から順に参照し,メロンを大箱に割り振っていく。大箱には箱連番を付与する。一つの大箱には,出荷条件である"メロンの合計重量が5kg以上"又は"メロンの個数が4個"のどちらかを満たすまでメロンを割り振る。ワークシート"重量計算表"の例を,図3に示す。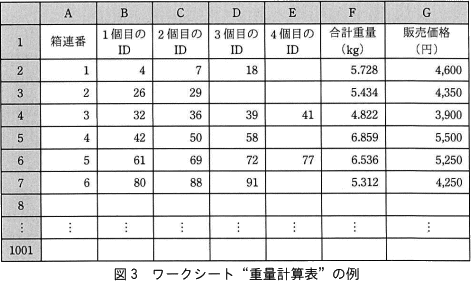 行1は見出し行である。マクロ Packing の実行前に,セル A2~F1001 には,空値が格納されている。セル G2~G1001 には,箱連番が示す大箱に割り振られたメロンの合計重量から販売価格を算出する式を入力しておく。この式は,合計重量を格納するセルが空値の場合は,空値を表示する。
行1は見出し行である。マクロ Packing の実行前に,セル A2~F1001 には,空値が格納されている。セル G2~G1001 には,箱連番が示す大箱に割り振られたメロンの合計重量から販売価格を算出する式を入力しておく。この式は,合計重量を格納するセルが空値の場合は,空値を表示する。
マクロ Packing は,処理(1)~(4)を実行する。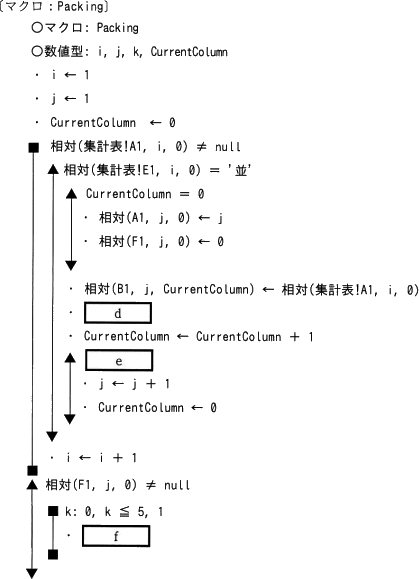
〔ワークシート:重量計算表〕
ワークシート"集計表"の行2以降のデータを上から順に参照し,メロンを大箱に割り振っていく。大箱には箱連番を付与する。一つの大箱には,出荷条件である"メロンの合計重量が5kg以上"又は"メロンの個数が4個"のどちらかを満たすまでメロンを割り振る。ワークシート"重量計算表"の例を,図3に示す。

マクロ Packing は,処理(1)~(4)を実行する。
- 列Aの行2以降には,1から順に箱連番を格納する。
- 列B~Eの行2以降には,箱連番が示す大箱に割り振られたメロンのIDを格納する。割り振られたメロンの個数が4未満だった場合,IDを格納しなかったセルは空値のままとなる。
- 列Fの行2以降には,箱連番が示す大箱に割り振られたメロンの合計重量を格納する。
- 割り振った結果,出荷条件を満たさない大箱に関する情報は,表示しないようにする。

d に関する解答群
- 相対(F1,i,0) ← 相対(F1,i,0)+相対(集計表!B1,1,0)
- 相対(F1,i,0) ← 相対(F1,i,0)+相対(集計表!B1,i,0)
- 相対(F1,i,0) ← 相対(F1,i,0)+相対(集計表!B1,j,0)
- 相対(F1,i,0) ← 相対(F1,j,0)+相対(集計表!B1,j,0)
- 相対(F1,j,0) ← 相対(F1,i,0)+相対(集計表!B1,0,0)
- 相対(F1,j,0) ← 相対(F1,j,0)+相対(集計表!B1,0,0)
- 相対(F1,j,0) ← 相対(F1,j,0)+相対(集計表!B1,i,0)
- 相対(F1,j,0) ← 相対(F1,j,0)+相対(集計表!B1,j,0)
e に関する解答群
- 論理積(相対(F1,j,0)=5,CurrentColumn=4)
- 論理積(相対(F1,j,0)=5,CurrentColumn≧4)
- 論理積(相対(F1,j,0)<5,CurrentColumn=4)
- 論理積(相対(F1,j,0)≧5,CurrentColumn<4)
- 論理和(相対(F1,j,0)=5,CurrentColumn≧4)
- 論理和(相対(F1,j,0)<5,CurrentColumn=4)
- 論理和(相対(F1,j,0)≧5,CurrentColumn=4)
- 論理和(相対(F1,j,0)≧5,CurrentColumn<4)
f に関する解答群
- 相対(A1,j,1) ← null
- 相対(A1,j,k) ← null
- 相対(A1,j,k) ← 相対(A1,j,k)+1
- 相対(A1,k,1) ← null
- 相対(A1,k,j) ← null
- 相対(A1,k,j) ← 相対(A1,k,j)+1
解答選択欄
- d:
- e:
- f:
解答
- d=キ
- e=キ
- f=イ
解説
〔dについて〕
選択肢を見ると、F1は合計重量が表示されるセル、集計表:B1は当該メロンの重量を保持するセルですから、dは箱にメロンを追加したときに合計重量を更新する処理であると見当が付きます。選択肢の各式で異なっているのは"相対"の第2引数である行位置だけです。
マクロ Paking では"集計表"の1行を処理し終わる度に i をインクリメントしているので、i が"集計表"における現在処理中の行番号、j が"重量計算表"における現在処理中の行番号を表していることになります。したがって、値を更新すべきセルと加えるべきメロンの重量は以下の式で参照できます。
∴d=キ
〔eについて〕
この分岐条件式が真のときには j をインクリメントしています。前述したように j は"重量計算表"で現在処理中の行番号を表す変数なので、これを加算するということは現在の箱が出荷条件を満たして、次の箱の処理に移るときです。
本文中には出荷条件として次の2つが記載されています。
∴e=キ
〔fについて〕
この処理を含むブロックは、"集計表"の全行の走査が終了した後に行う処理で、マクロ Paking の説明(4)の「割り振った結果,出荷条件を満たさない大箱に関する情報は,表示しないようにする」を実現するものとなります。
"集計表"の全行の走査が終了した段階で、ちょうど出荷条件を満たす箱が完成するとは限りません。この場合、"重量計算量"の最後に処理中であった行には箱連番やメロンのIDが中途半端に表示された状態になっています。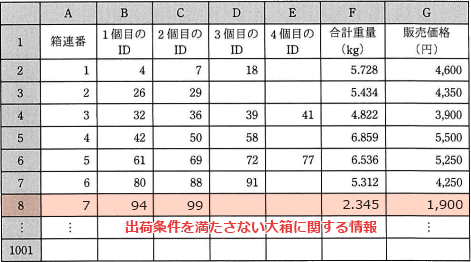 これを表示しないようにするには、"重量計算量"の処理中の行のA列(箱連番)~F列(合計重量)に null を代入する必要があります。
これを表示しないようにするには、"重量計算量"の処理中の行のA列(箱連番)~F列(合計重量)に null を代入する必要があります。
"相対"は第1引数で行位置、第2引数で列位置を指定するので、行位置には"重量計算量"の処理中の行番号を保持する j を、列位置には繰返し処理によって0~5まで変化する k を指定します。これによって、相対(A1, j, 0)~相対(A1, j, 5) にnullが代入され、出荷条件を満たしていない最終行(出荷条件を満たさない大箱に関する情報)が非表示化されます。
∴f=イ
選択肢を見ると、F1は合計重量が表示されるセル、集計表:B1は当該メロンの重量を保持するセルですから、dは箱にメロンを追加したときに合計重量を更新する処理であると見当が付きます。選択肢の各式で異なっているのは"相対"の第2引数である行位置だけです。
マクロ Paking では"集計表"の1行を処理し終わる度に i をインクリメントしているので、i が"集計表"における現在処理中の行番号、j が"重量計算表"における現在処理中の行番号を表していることになります。したがって、値を更新すべきセルと加えるべきメロンの重量は以下の式で参照できます。
- "重量計算表"で更新すべきセル
- 相対(F1, j, 0)
- "集計表"で処理中のメロンの重量
- 相対(B1, i, 0)
∴d=キ
〔eについて〕
この分岐条件式が真のときには j をインクリメントしています。前述したように j は"重量計算表"で現在処理中の行番号を表す変数なので、これを加算するということは現在の箱が出荷条件を満たして、次の箱の処理に移るときです。
本文中には出荷条件として次の2つが記載されています。
- メロンの合計重量が5kg以上
- メロンの個数が4個
- 相対(F1, j, 0) ≧ 5
- currentColumn = 4
∴e=キ
〔fについて〕
この処理を含むブロックは、"集計表"の全行の走査が終了した後に行う処理で、マクロ Paking の説明(4)の「割り振った結果,出荷条件を満たさない大箱に関する情報は,表示しないようにする」を実現するものとなります。
"集計表"の全行の走査が終了した段階で、ちょうど出荷条件を満たす箱が完成するとは限りません。この場合、"重量計算量"の最後に処理中であった行には箱連番やメロンのIDが中途半端に表示された状態になっています。

"相対"は第1引数で行位置、第2引数で列位置を指定するので、行位置には"重量計算量"の処理中の行番号を保持する j を、列位置には繰返し処理によって0~5まで変化する k を指定します。これによって、相対(A1, j, 0)~相対(A1, j, 5) にnullが代入され、出荷条件を満たしていない最終行(出荷条件を満たさない大箱に関する情報)が非表示化されます。
∴f=イ
