HOME»基本情報技術者平成23年秋期問題»午後問1
基本情報技術者過去問題 平成23年秋期 午後問1
⇄問題文と設問を画面2分割で開く⇱問題PDF問1 ハードウェア
A/D変換に関する次の記述を読んで，設問1～3に答えよ。
A/D変換とは，アナログ信号をデジタル信号に変換することであり，標本化，量子化，符号化の3段階で処理する。直流の電圧を例にnビットのA/D変換を説明する。
A/D変換とは，アナログ信号をデジタル信号に変換することであり，標本化，量子化，符号化の3段階で処理する。直流の電圧を例にnビットのA/D変換を説明する。
- 標本化
標本化では，時間的に連続したアナログ信号である電圧を一定の時間間隔で測定する。図1では，時間軸を t0，t1，… と等間隔dで区切り，各時刻での電圧を v(t0)，v(t1)，… と表す。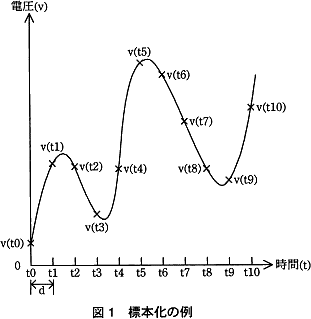
- 量子化
量子化では，(1)で標本化して得られた電圧 v(t0)，v(t1)，… を刻み幅qの整数倍の値で近似する。
量子化を行う場合，まず測定する電圧の最大幅FSRを決める。次に，n ビットで量子化するために，FSRを(2n－1)等分して刻み幅qを求める。このとき，刻み幅 q＝FSR／(2n－1)となる。
量子化において，近似値として用いられる電圧の値を，小さい方から順に v0＝0，v1＝q，…，vmax＝(2n－1)q としたとき，時刻 tm において標本化で測定されたアナログ信号の電圧 v(tm) について，次の条件を満たすようなN(Nは0以上の整数)を見つけ，電圧N×qを電圧v(tm)の測定値とする。これをnビット量子化という。
N×q－q／2≦v(tm)＜N×q＋q／2
すなわち，図2右のように電圧軸を刻み幅qで v0，v1，…，vmax の電圧に分割しておき，v(t0)，v(t1)，… のそれぞれについて，v0～vmaxのうちで最も近い電圧を測定値とする。例えば，v(t3)の測定値はv2となる。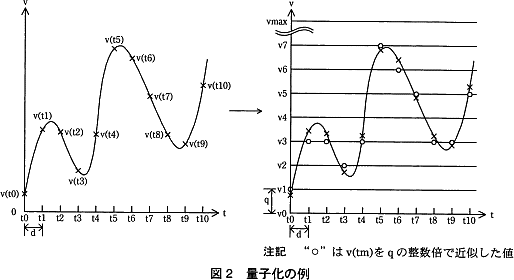
- 符号化
符号化では，(2)の量子化で用いた電圧 v0，v1，…，vmax に2進符号を対応付ける。この符号によって，各測定値を表す。
設問1
図2左の電圧 v(t0)，v(t1)，…，v(t10)だけの符号化を考える。 図2右の電圧 v0，v1，…，v7を2進符号000，001，…，111に順に対応付けた場合を表1に示す。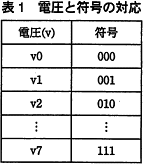
図2左の v(t0)，v(t1)，…，v(t10)の各測定値を，表1に基づいて符号化すると 表2のようになる。表2中の に入れる正しい答えを，解答群の中から選べ。
a，b に関する解答群
- 011
- 100
- 101
- 110
- 111
解答選択欄
- a:
- b:
解答
- a=エ
- b=ウ
解説
〔aについて〕
図2の右の図から t6 の測定値は v6 と読み取れます。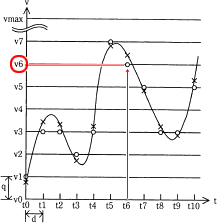
表1見るとv0が000(10進数で0)、v7が111(10進数で7)にそれぞれ対応しているため、これに従うと v6 の符号は"6"を2進数で表した「110」になります。
6＝22＋21＝(110)2
∴a＝エ：110
〔bについて〕
図2の右の図から t10 の測定値は v5 と読み取れます。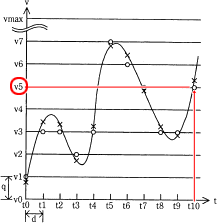
したがってbは v5 の"5"を2進数で表した「101」になります。
5＝22＋20＝(101)2
∴b＝ウ：101
図2の右の図から t6 の測定値は v6 と読み取れます。
6＝22＋21＝(110)2
∴a＝エ：110
〔bについて〕
図2の右の図から t10 の測定値は v5 と読み取れます。
5＝22＋20＝(101)2
∴b＝ウ：101
設問2
次の記述中の に入れる正しい答えを，解答群の中から選べ。
アナログ信号の電圧の範囲が0～9Vであるとき，FSRを 9V とし，4ビットで量子化した場合，qはcVである。アナログ信号の電圧7.49…Vの測定値はdVとなり，表1の場合と同様に2進符号 0000，0001，…，1111 に順に対応付けて符号化するとeとなる。
アナログ信号の電圧の範囲が0～9Vであるとき，FSRを 9V とし，4ビットで量子化した場合，qはcVである。アナログ信号の電圧7.49…Vの測定値はdVとなり，表1の場合と同様に2進符号 0000，0001，…，1111 に順に対応付けて符号化するとeとなる。
c，d に関する解答群
- 0.5625
- 0.6
- 1.2
- 2.25
- 5.5
- 7.0
- 7.2
- 7.5
- 7.8
- 8.0
e に関する解答群
- 1010
- 1011
- 1100
- 1101
- 1110
解答選択欄
- c:
- d:
- e:
解答
- c=イ
- d=キ
- e=ウ
解説
〔cについて〕
刻み幅qは、FSRを(2n－1)等分して求めるので、FSR=9、量子化ビットn=4の時のqは以下のように計算できます。
9／(24－1)＝9／15＝0.6
よってqは0.6Vです。
∴c＝イ：0.6
〔dについて〕
まず7.49Vを刻み幅qで割ると、
7.49÷0.6＝12.48333…
この値に最も近い整数は12なので、7.49Vの測定値としてv12が採用され、その電圧の値は以下のように計算できます。
0.6×12＝7.2(V)
∴d＝キ：7.2
〔eについて〕
dより測定値はv12なので、対応表に従い"12"を2進数で表したものが符号になります。
12＝23＋22＝(1100)2
したがって符号は「1100」になります。
∴e＝ウ：1100
刻み幅qは、FSRを(2n－1)等分して求めるので、FSR=9、量子化ビットn=4の時のqは以下のように計算できます。
9／(24－1)＝9／15＝0.6
よってqは0.6Vです。
∴c＝イ：0.6
〔dについて〕
まず7.49Vを刻み幅qで割ると、
7.49÷0.6＝12.48333…
この値に最も近い整数は12なので、7.49Vの測定値としてv12が採用され、その電圧の値は以下のように計算できます。
0.6×12＝7.2(V)
∴d＝キ：7.2
〔eについて〕
dより測定値はv12なので、対応表に従い"12"を2進数で表したものが符号になります。
12＝23＋22＝(1100)2
したがって符号は「1100」になります。
∴e＝ウ：1100
設問3
次の記述中の に入れる正しい答えを，解答群の中から選べ。
FSRが1,022ミリVであるアナログ信号の電圧を，50ミリ秒間隔で5秒間標本化した。このとき，A/D変換後の総データ量を1,000ビット以内に納めることができる刻み幅qの最小値はfミリVである。
FSRが1,022ミリVであるアナログ信号の電圧を，50ミリ秒間隔で5秒間標本化した。このとき，A/D変換後の総データ量を1,000ビット以内に納めることができる刻み幅qの最小値はfミリVである。
f に関する解答群
- 0.1
- 0.5
- 1.0
- 1.5
- 2.0
- 2.5
- 3.0
解答選択欄
- f:
解答
- f=オ
解説
まず例として200ミリ間隔で1秒間の測定を行うことを考えてみると、標本化の回数は次のように6回になります。
(測定時間÷標本化間隔)＋1
この式を使用すると標本化の間隔は50ミリ秒、測定時間は5秒(5,000ミリ秒)なので、
(5,000÷50)＋1＝101(回)
標本化の回数は101回と求められます。
さらに標本化を101回行い、総データ量を1,000ビット以下に収めるためには、
1,000÷101＝9.900…(ビット)
という計算より測定1回あたりに使えるビット数は最大で9ビットとわかります。刻み幅qは「FSR／(2n－1)」で求めるため、この式に FSR=1,022、n=9 を代入すると、
q＝1,022／(29－1)
q＝1,022／(512－1)
q＝1,022／511
q＝2
したがって刻み幅qの最小値は2.0ミリVです。
∴f＝オ：2.0
- 0ミリ秒
- 200ミリ秒
- 400ミリ秒
- 600ミリ秒
- 800ミリ秒
- 1000ミリ秒(1秒)
(測定時間÷標本化間隔)＋1
この式を使用すると標本化の間隔は50ミリ秒、測定時間は5秒(5,000ミリ秒)なので、
(5,000÷50)＋1＝101(回)
標本化の回数は101回と求められます。
さらに標本化を101回行い、総データ量を1,000ビット以下に収めるためには、
1,000÷101＝9.900…(ビット)
という計算より測定1回あたりに使えるビット数は最大で9ビットとわかります。刻み幅qは「FSR／(2n－1)」で求めるため、この式に FSR=1,022、n=9 を代入すると、
q＝1,022／(29－1)
q＝1,022／(512－1)
q＝1,022／511
q＝2
したがって刻み幅qの最小値は2.0ミリVです。
∴f＝オ：2.0