HOME»基本情報技術者平成26年秋期問題»午後問13
基本情報技術者過去問題 平成26年秋期 午後問13
⇄問題文と設問を画面2分割で開く⇱問題PDF⇱表計算ソフトの機能・用語問13 ソフトウェア開発(表計算)
次の表計算のワークシート及びマクロの説明を読んで,設問1,2に答えよ。
〔表計算の説明〕
鉄道会社Y社では,表計算ソフトを使って乗車駅と降車駅を入力すると鉄道路線における駅間の距離(以下,乗車距離という)と運賃を表示するプログラムを作成した。
乗車駅から降車駅までの間(以下,乗車区間という)にある隣接駅間距離を選び出し,それらを合計したものを乗車距離とする。乗車距離(ワークシート"鉄道運賃"のセル B3)を求めるために,ワークシート"路線情報"と "鉄道運賃"に(1)~(3)の手順で式の入力を行う。
区分距離と区分運賃を計算し,基本運賃と全ての区分運賃を合計したものを運賃とする。運賃(ワークシート"鉄道運賃"のセル B4)を求めるために,ワークシート"運賃情報"と"鉄道運賃"に(1)~(4)の手順で式の入力を行う。
〔表計算の説明〕
鉄道会社Y社では,表計算ソフトを使って乗車駅と降車駅を入力すると鉄道路線における駅間の距離(以下,乗車距離という)と運賃を表示するプログラムを作成した。
- 鉄道路線は,隣接駅間の距離(以下,隣接駅間距離という)が 5km を超えず,分岐をもたない全長 94.2km の単一路線であり,起点駅から終点駅まで32の駅から成る。
- 各駅には"001"~"032"の駅コードが割り付けられている。
- ワークシート"鉄道運賃"に乗車駅の駅コード(セルB1)と降車駅の駅コード(セルB2)を入力すると,乗車距離(セルB3)と運賃(セルB4)が表示される。乗車駅と降車駅の駅コードは,鉄道路線の各駅に割り付けられた駅コードのリストから選択して入力するようになっている。ワークシート"鉄道運賃"の例を図1に示す。

- 駅コードと隣接駅間距離は,起点駅から終点駅に向かってワークシート"路線情報"の列Aと列Bに順に格納されている。ワークシート"路線情報"の例を図2に示す。
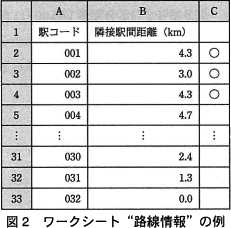
- ワークシートの各行の隣接駅間距離には,その行の駅コードに対応する駅から次行の駅コードに対応する駅までの距離(単位はkm)が格納されている。例えば,駅コード"002"と駅コード"003"の駅間の距離は,セル B3 に格納されている3.0である。終点駅の駅コードに対応する行の隣接駅間距離(セルB33)には0.0が格納されている。
- 列Cは乗車距離計算のための作業領域に用いる。
- 運賃は,乗車距離に関係なく一律に定められている基本運賃100円と,乗車距離に応じて決まる距離運賃とを合計した額である。
- 距離運賃は,決められた四つの距離の範囲で乗車距離を区分し,決められた計算方法で区分ごとの運賃(以下,区分運賃という)を計算し,それらを合計した額である。
- 各区分には1~4の番号(以下,区分番号という)が割り付けられている。各区分の距離の範囲は表1のとおりである。
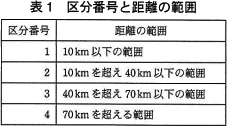
- 乗車距離を,決められた四つの距離の範囲で区分し,区分ごとの距離(以下,区分距離という)に分ける。例えば,乗車距離が11.6kmの場合,区分番号1の区分距離10kmと,区分番号2の区分距離1.6km(11.6km-10km)に分ける。
- 区分ごとに,運賃計算の基準となる単位距離が決められている。区分,単位距離と単位運賃の関係を表2に示す。区分距離の端数は単位距離に切り上げ,単位距離ごとに単位運賃を加算する。
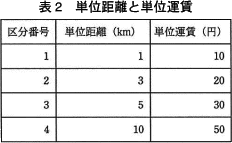
- 各区分には1~4の番号(以下,区分番号という)が割り付けられている。各区分の距離の範囲は表1のとおりである。
- 例えば,乗車距離が11.6kmである駅コード"004"から駅コード"001"までの 運賃は,次のように求める。ここで,計算式中の"切上げ(X,0)"は,Xの小数点以下を 切り上げた値を表す。
- 区分番号1の区分運賃は,1kmまでごとに10円を加算し,次の式で求める。
10円×切上げ(10km÷1km,0)=100円 - 区分番号2の区分運賃は,3kmまでごとに20円を加算し,次の式で求める。
20円×切上げ((11.6km-10km)÷3km,0)=20円 - 運賃は,基本運賃100円と距離運賃120円(①,②で求めた区分運賃の合計額)を合計した220円になる。
- 区分番号1の区分運賃は,1kmまでごとに10円を加算し,次の式で求める。
- 基本運賃と各区分の区分番号,距離の範囲の上限(以下,上限距離という),単位距離及び単位運賃を格納したワークシート"運賃情報"の例を図3に示す。
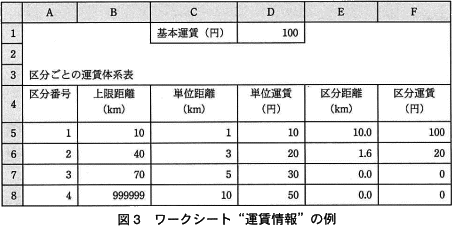
- セル D1 には,基本運賃が格納されている。
- 区分ごとの運賃体系表(セル A4~D8 )のセル A5~D8 には,各区分の区分番号,上限距離,単位距離及び単位運賃が区分番号の昇順に格納されている。
- 区分番号4の上限距離には,999999 が格納されている。
- 列E,Fには,各区分の区分距離と区分運賃が表示される。
乗車駅から降車駅までの間(以下,乗車区間という)にある隣接駅間距離を選び出し,それらを合計したものを乗車距離とする。乗車距離(ワークシート"鉄道運賃"のセル B3)を求めるために,ワークシート"路線情報"と "鉄道運賃"に(1)~(3)の手順で式の入力を行う。
- 乗車区間の判別に当たり,ワークシート"路線情報"のセル C34 とセル C35 を 使用する。乗車駅及び降車駅の駅コードを利用するために,ワークシート"路線情報"のセル C34 に次の式を入力し,セル C35 に複写する。
照合一致(鉄道運賃!B1,A$2~A$33,0) - ワークシート"路線情報"のセル C2 に次の式を入力し,セル C3~C32 に複写する。
IF(a(b,c),'○',null) - 乗車距離を求めるために,ワークシート"鉄道運賃"のセル B3 に次の式を入力する。
条件付合計(路線情報!C2~C32,='○',路線情報!B2~B32)
区分距離と区分運賃を計算し,基本運賃と全ての区分運賃を合計したものを運賃とする。運賃(ワークシート"鉄道運賃"のセル B4)を求めるために,ワークシート"運賃情報"と"鉄道運賃"に(1)~(4)の手順で式の入力を行う。
- 区分番号1の区分距離を求めるために,ワークシート"運賃情報"のセル E5 に次の式を入力する。
IF(鉄道運賃!B3≦B5,鉄道運賃!B3,B5) - 区分番号2~4の区分距離を求めるために,ワークシート"運賃情報"のセル E6 に次の式を入力し,セル E7,E8 に複写する。
IF(鉄道運賃!B$3≦B6,鉄道運賃!B$3,B6)-d - 区分運賃を求めるために,ワークシート"運賃情報"のセル F5 に次の式を入力し,セル F6~F8 に複写する。
e - 乗車区間の運賃を求めるために,ワークシート"鉄道運賃"のセル B4 に次の式を入力する。
運賃情報!D1+合計(運賃情報!F5~F8)
設問1
乗車距離の計算,運賃の計算に関する説明文中の に入れる正しい答えを,解答群の中から選べ。
a に関する解答群
- 論理積
- 論理和
b に関する解答群
- 照合一致(A2,A$2~A$33,0)<最小(C$34~C$35)
- 照合一致(A2,A$2~A$33,0)≦最小(C$34~C$35)
- 照合一致(A2,A$2~A$33,0)>最小(C$34~C$35)
- 照合一致(A2,A$2~A$33,0)≧最小(C$34~C$35)
c に関する解答群
- 照合一致(A2,A$2~A$33,0)<最大(C$34~C$35)
- 照合一致(A2,A$2~A$33,0)≦最大(C$34~C$35)
- 照合一致(A2,A$2~A$33,0)>最大(C$34~C$35)
- 照合一致(A2,A$2~A$33,0)≧最大(C$34~C$35)
d に関する解答群
- B5
- E5
- 合計(B$5~B5)
- 合計(B$5~B$8)
- 合計(E5~E$8)
- 合計(E$5~E5)
e に関する解答群
- 切上げ(B5,0)/C5*D5
- 切上げ(B5/C5,0)*D5
- 切上げ(E5,0)/C5*D5
- 切上げ(E5/C5,0)*D5
- 切捨て(B5/C5+1,0)*D5
- 切捨て(E5/C5+1,0)*D5
解答選択欄
- a:
- b:
- c:
- d:
- e:
解答
- a=ア
- b=エ
- c=ア
- d=カ
- e=エ
解説
〔abcについて〕
ワークシート"路線情報"のセル C2(作業領域)に設定するIF文を整理すると以下のようになります。論理式の結果が真の場合に、'○'を表示するものを選択する必要があります。
次に'○'を表示する意味を考えます。'○'を付けたセルは〔運賃の計算〕(3)の条件付合計で値を合計する条件となっていて、'○'が付いている行の'隣接駅間距離'の合計を乗車駅と降車駅の間の乗車距離としています。B列(隣接駅間距離)には「その行の駅コードに対応する駅から次行の駅コードに対応する駅までの距離(単位はkm)が格納されている」ので、図1の乗車駅'001'、降車駅'004'の場合には、図2のように駅コード'001'~'003'の3行に'○'が付くのが適切です。つまり、'○'を付ける条件は「駅コードが乗車駅(駅コード)以上、かつ、駅コードが降車駅(駅コード)未満」ということになります。
ここで駅コード'004'の駅から'001'の駅まで乗車するように、乗車駅(駅コード)>降車駅(駅コード)の場合も想定できるので、乗車駅としては C34 と C35 の小さい方、降車駅にはC34 と C35 の大きい方を使う必要があります。したがって、
[a]は「ア」の論理積、[b]は比較演算子が'≧'の「エ」、[c]は比較演算子が'<'の「ア」が適切です。
∴a=ア:論理積
b=エ:照合一致(A2,A$2~A$33,0)≧最小(C$34~C$35)
c=ア:照合一致(A2,A$2~A$33,0)<最大(C$34~C$35)
〔dについて〕
ワークシート"運賃情報"のE列には区分ごとの距離を求めています。〔表計算の説明〕(6)①「区分番号と距離の範囲」では以下の記載があるので、区分1と2以降では処理が異なります。 区分番号2~4に入力する式は、乗車距離(鉄道運賃!B$3)と上限距離(B6)からその区分の距離を求める式になっている必要があります。
区分番号2~4に入力する式は、乗車距離(鉄道運賃!B$3)と上限距離(B6)からその区分の距離を求める式になっている必要があります。
消去法ではありますが、図3の例(乗車距離11.6km)で各式を入力したときにセル E7 の値が0になるかどうかを見ることで素早く正解を導けます。ここで、セル E7 では乗車距離≦上限距離なのでIF文は11.6を返します。
〔eについて〕
〔表計算の説明〕(7)には以下の説明があります。
② 区分番号2の区分運賃は,3kmまでごとに20円を加算し,次の式で求める。
20円×切上げ((11.6km-10km)÷3km,0)=20円
上の式の数値はそれぞれ、 ∴e=エ:切上げ(E5/C5,0)*D5
∴e=エ:切上げ(E5/C5,0)*D5
ワークシート"路線情報"のセル C2(作業領域)に設定するIF文を整理すると以下のようになります。論理式の結果が真の場合に、'○'を表示するものを選択する必要があります。
論理式:a (b, c)
真の場合:文字列'○'を表示する。
偽の場合:何も表示しない(空値を表示)。
まず最初に[b]と[c]の選択肢中で参照しているセル C34 および C35 に何が格納されているのかを確認します。この2つのセルには〔運賃の計算〕(2)で以下の照合一致の式が入力されています(複写されるのでセル C35 ではB1→B2になります)。真の場合:文字列'○'を表示する。
偽の場合:何も表示しない(空値を表示)。
照合一致(鉄道運賃!B1,A$2~A$33,0)
照合一致は、セル範囲の中での指定された値の位置を返す関数ですので、セル C34 には駅コード(B2~B33)内での乗車駅(駅コード)の相対位置、セル C35 には駅コード(B2~B33)内での降車駅(駅コード)の相対位置が入っています。例えば図1のように乗車駅(駅コード)が'001'、降車駅(駅コード)が'004'ならば、セル C34 には1が、セル C35 には4が格納されています。次に'○'を表示する意味を考えます。'○'を付けたセルは〔運賃の計算〕(3)の条件付合計で値を合計する条件となっていて、'○'が付いている行の'隣接駅間距離'の合計を乗車駅と降車駅の間の乗車距離としています。B列(隣接駅間距離)には「その行の駅コードに対応する駅から次行の駅コードに対応する駅までの距離(単位はkm)が格納されている」ので、図1の乗車駅'001'、降車駅'004'の場合には、図2のように駅コード'001'~'003'の3行に'○'が付くのが適切です。つまり、'○'を付ける条件は「駅コードが乗車駅(駅コード)以上、かつ、駅コードが降車駅(駅コード)未満」ということになります。
ここで駅コード'004'の駅から'001'の駅まで乗車するように、乗車駅(駅コード)>降車駅(駅コード)の場合も想定できるので、乗車駅としては C34 と C35 の小さい方、降車駅にはC34 と C35 の大きい方を使う必要があります。したがって、
論理積(
当該行の駅コードの位置≧小さい方の駅コードの位置,
当該行の駅コードの位置<大きい方の駅コードの位置
)
という式で'○'を付けるセルを判定でできます。当該行の駅コードの位置≧小さい方の駅コードの位置,
当該行の駅コードの位置<大きい方の駅コードの位置
)
[a]は「ア」の論理積、[b]は比較演算子が'≧'の「エ」、[c]は比較演算子が'<'の「ア」が適切です。
∴a=ア:論理積
b=エ:照合一致(A2,A$2~A$33,0)≧最小(C$34~C$35)
c=ア:照合一致(A2,A$2~A$33,0)<最大(C$34~C$35)
〔dについて〕
ワークシート"運賃情報"のE列には区分ごとの距離を求めています。〔表計算の説明〕(6)①「区分番号と距離の範囲」では以下の記載があるので、区分1と2以降では処理が異なります。

消去法ではありますが、図3の例(乗車距離11.6km)で各式を入力したときにセル E7 の値が0になるかどうかを見ることで素早く正解を導けます。ここで、セル E7 では乗車距離≦上限距離なのでIF文は11.6を返します。
- 11.6から B6 の値(40)を差し引くと「-28.4」になります(×)。
- 11.6から E6 の値(1.6)を差し引くと「10」になります(×)。
- 11.6から B5~B6 の合計値(50)を差し引くと「-38.4」になります(×)。
- 11.6から B5~B8 の合計値(1,000,119)を差し引くと「-1,000,107.4」になります(×)。
- 11.6から E6~E8 の合計値(1.6)を差し引くと「10」になります(×)。
- 11.6から E5~E6 の合計値(11.6)を差し引くと「0」になります(○)。
値が0になるのでこれが正解です。
〔eについて〕
〔表計算の説明〕(7)には以下の説明があります。
② 区分番号2の区分運賃は,3kmまでごとに20円を加算し,次の式で求める。
20円×切上げ((11.6km-10km)÷3km,0)=20円
上の式の数値はそれぞれ、
- 20円 … 単位運賃(D5)
- (11.6km-10km) …区分距離(E5)
- 3km … 単位距離(C5)

設問2
Y社では,区分運賃を見直すことによる運賃改定を行うことにした。ただし,区分ごとの単位距離と単位運賃は変更せず,距離の範囲だけを見直す。これに伴い,ワークシート"運賃情報"の区分番号1~3の上限距離(セルB5~B7)の値を変更するためのマクロを作成し,ワークシート"運賃情報"に格納した。マクロ Change_SectionInfo に関する説明を読んで,マクロ中の に入れる正しい答えを,解答群の中から選べ。ここで,g1 と g2に入れる答えは,g に関する解答群の中から組合せとして正しいものを選ぶものとする。
〔距離の範囲見直しの説明〕
〔距離の範囲見直しの説明〕
- 少なくとも隣接駅間距離は,区分番号1の距離の範囲に入るようにする。
- 隣接駅間距離の中で最長の距離を求める。
- 求めた距離の小数点以下を切り上げた値を,区分番号1の新たな上限距離とする。
- 五つ離れた駅までの距離は,区分番号2の距離の範囲に入るようにする。
- 鉄道路線上のそれぞれの駅から五つ離れた駅までの距離を計算し,その中で最長の距離を求める。
- 区分番号1の新たな上限距離に区分番号2の単位距離の倍数を加えた値でかつ,①で求めた距離以上となる最小値を,区分番号2の新たな上限距離とする。
- 鉄道路線の全区間(起点駅から終点駅まで)の距離の50%以下の距離は,区分番号3の距離の範囲に入るようにする。
- 鉄道路線の全区間の50%の距離を求める。
- 区分番号2の新たな上限距離に区分番号3の単位距離の倍数を加えた値で,かつ,①で求めた距離以上となる最小値を,区分番号3の新たな上限距離とする。

f に関する解答群
- J:0,J≦4
- J:1,J≦4
- J:0,J≦5
- J:1,J≦5
- J:0,J≦31
- J:1,J≦31
g に関する解答群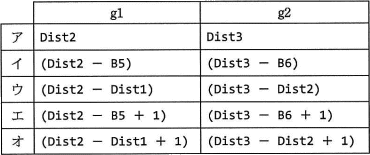

解答選択欄
- f:
- g:
解答
- f=イ
- g=イ
解説
〔fについて〕
マクロ中のループ処理は〔距離の範囲見直しの説明〕(2)①の「鉄道路線上のそれぞれの駅から五つ離れた駅までの距離を計算し,その中で最長の距離を求める」部分です。ここでは、駅コード001の行から駅コード026までの駅について、5つ先の駅までの距離を Sum2 に求め、それがより長い距離だったときに Dist2 を更新することで、ループ終了時に Dist2 に"最長の距離"が格納されるようになっています。
駅コード001から5つ先の駅までの距離は、ワークシート"路線情報"の B2~B6 の合計、駅コード002から5つ先の駅までの距離は、ワークシート"路線情報"の B3~B7 の合計というように、その行を含めて5行分の隣接駅間距離の値を合計することで、始点となる駅から五つ離れた駅までの距離を求められます。[f]の直前の行で Sum2 に始点となる行の距離を格納しているので、続くループ文では残る4行分について距離を加算すれば良いことになります。ループ変数 I を基準として相対を使い、I+1、I+2、I+3、I+4 で4行を参照したいので、Jは1から4まで増やすことになります。
∴f=イ:J:1,J≦4
〔gについて〕
[g1]を含む文は〔距離の範囲見直しの説明〕(2)②の「区分番号1の新たな上限距離に区分番号2の単位距離の倍数を加えた値でかつ,①で求めた距離以上となる最小値を,区分番号2の新たな上限距離とする」部分です。ややこしい表現ですが、
B5+(C6×n)≧Dist2
これを変形すると、
C6×n≧Dist2-B5
n≧(Dist2-B5)/C6
という式が得られます。これにより最初の式の左辺が Dist2 以上になるには、nが (Dist2-B5)/C6 以上でなければならないことがわかります。よって、切上げによって (Dist2-B5)/C6 以上となる最小の整数を求め、それを単位距離(C6)の乗数nとすれば「①で求めた距離以上となる最小値」が計算できます。したがって[g1]には「Dist2-B5」が入ります。[g2]についても同じ考え方で「Dist3-B6」が入ります。
∴g=イ
マクロ中のループ処理は〔距離の範囲見直しの説明〕(2)①の「鉄道路線上のそれぞれの駅から五つ離れた駅までの距離を計算し,その中で最長の距離を求める」部分です。ここでは、駅コード001の行から駅コード026までの駅について、5つ先の駅までの距離を Sum2 に求め、それがより長い距離だったときに Dist2 を更新することで、ループ終了時に Dist2 に"最長の距離"が格納されるようになっています。
駅コード001から5つ先の駅までの距離は、ワークシート"路線情報"の B2~B6 の合計、駅コード002から5つ先の駅までの距離は、ワークシート"路線情報"の B3~B7 の合計というように、その行を含めて5行分の隣接駅間距離の値を合計することで、始点となる駅から五つ離れた駅までの距離を求められます。[f]の直前の行で Sum2 に始点となる行の距離を格納しているので、続くループ文では残る4行分について距離を加算すれば良いことになります。ループ変数 I を基準として相対を使い、I+1、I+2、I+3、I+4 で4行を参照したいので、Jは1から4まで増やすことになります。
∴f=イ:J:1,J≦4
〔gについて〕
[g1]を含む文は〔距離の範囲見直しの説明〕(2)②の「区分番号1の新たな上限距離に区分番号2の単位距離の倍数を加えた値でかつ,①で求めた距離以上となる最小値を,区分番号2の新たな上限距離とする」部分です。ややこしい表現ですが、
- 区分番号1の新たな上限距離 → 直前行で求めたB5
- 区分番号2の単位距離 → C6
- ①で求めた距離 → Dist2
B5+(C6×n)≧Dist2
これを変形すると、
C6×n≧Dist2-B5
n≧(Dist2-B5)/C6
という式が得られます。これにより最初の式の左辺が Dist2 以上になるには、nが (Dist2-B5)/C6 以上でなければならないことがわかります。よって、切上げによって (Dist2-B5)/C6 以上となる最小の整数を求め、それを単位距離(C6)の乗数nとすれば「①で求めた距離以上となる最小値」が計算できます。したがって[g1]には「Dist2-B5」が入ります。[g2]についても同じ考え方で「Dist3-B6」が入ります。
∴g=イ
