HOME»基本情報技術者平成30年秋期問題»午後問8
基本情報技術者過去問題 平成30年秋期 午後問8
⇄問題文と設問を画面2分割で開く⇱問題PDF問8 データ構造及びアルゴリズム
次のプログラムの説明及びプログラムを読んで,設問1~3に答えよ。
整数式を受け取って,その値を返すプログラムである。例えば,例1に示す整数式を受け取ると,その値50を返す。
例1: 2×(34-(5+67)÷8)
〔プログラムの説明〕
〔プログラム(解析処理部分)の説明〕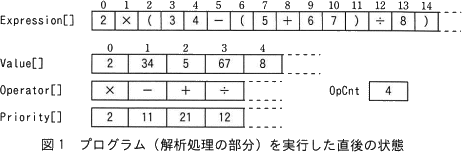
 〔プログラム(計算処理の部分)の説明〕
〔プログラム(計算処理の部分)の説明〕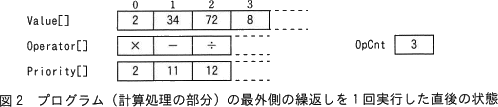

整数式を受け取って,その値を返すプログラムである。例えば,例1に示す整数式を受け取ると,その値50を返す。
例1: 2×(34-(5+67)÷8)
〔プログラムの説明〕
- 整数式は,文字の列で与えられる。整数式は,次のもので構成される。
- 符号のない数字。0~9の並び
- 演算子: +,-,×,÷
- 括弧: (,)
- 引数 Expression[ ] で整数式を,引数 ExpLen で整数式の文字数を,それぞれ受け取る。
- プログラム中の破線で囲んだ解析処理の部分では,受け取った整数式を解析し,計算に必要な情報を配列及び変数に設定する。
- プログラム中の破線で囲んだ計算処理の部分では,(3)で設定した情報を用いて,整数式の値を計算する。整数式の値は,Value[0] に得られる。
- 各配列の添字は,0から始まる。各配列の要素数は,十分に大きいものとする。
- 受け取った整数式に誤りはないものとする。また,計算の過程で,あふれやゼロ除算は発生しないものとする。

〔プログラム(解析処理部分)の説明〕
- Expression[ ] で渡された整数式を解析し,計算に必要な情報を配列 Operator[ ],Priority[ ],Value[ ] 及び変数 OpCnt に設定する。関数 int() は,引数の数字が表す値を整数型で返す。
- 例1の整数式について,プログラム(解析処理の部分)を実行した直後の各配列及び変数の状態を,図1に示す。


- 整数式の値を計算していく。図1に示す各配列及び変数の状態から,プログラム(計算処理の部分)の最外側の繰返しを1回実行した直後の各配列及び変数の状態を,図2に示す。


設問1
プログラム(解析処理の部分)に関する次の記述中の に入れる正しい答えを,解答群の中から選べ。
プログラム(解析処理の部分)の行①~④で用いている定数について考察する。
まず,行③及び④の処理では,定数として10を用いているが,この定数は10である必要はない。このプログラムにおいては,定数がaであれば常に正しい演算順序が保証される。
また,行①及び②の処理では,定数として1及び2を用いているが,次に示すように書き換えることが可能である。ここで,priLow 及び priHigh は整数の定数を表し,その値は priLow<priHigh とする。
プログラム(解析処理の部分)の行①~④で用いている定数について考察する。
まず,行③及び④の処理では,定数として10を用いているが,この定数は10である必要はない。このプログラムにおいては,定数がaであれば常に正しい演算順序が保証される。
また,行①及び②の処理では,定数として1及び2を用いているが,次に示すように書き換えることが可能である。ここで,priLow 及び priHigh は整数の定数を表し,その値は priLow<priHigh とする。
- ①→ ・Priority[OpCnt] ← nest+priLow
- ②→ ・Priority[OpCnt] ← nest+priHigh
a に関する解答群
- 1以上
- 2以上
- 11以下
- 12以下
b に関する解答群
- priHigh以上
- priHigh+1以上
- priHigh-priLow以上
- priHigh-priLow+1以上
解答選択欄
- a:
- b:
解答
- a=イ
- b=エ
解説
〔aについて〕
まずは、行③及び④の処理において定数の10を加減する対象となっている変数 nest の役割について考えてみましょう。nest は、行①及び②の処理において、Priority[] に格納される値のベースに使われています。Priority[]は、その名前(priority:優先度)が示すように演算の優先順位を保持する配列で、〔プログラム(計算処理の部分)〕ではこの値が大きい演算から先に順番する処理になっています。
行③では、式中に"("が見つかると nest に10を加えています。逆に行④では")"が見つかると10を引いています。つまり nest は、括弧の中の演算の優先度を高くするための変数であり、括弧の内部であるほど nest の値も大きくなります。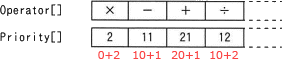 式を計算するときには、より括弧の内側の演算を優先して処理します。また、加減算よりも乗除算を優先するルールになっています。このため、式が正しく評価されるためには、優先順位が「括弧外の加減算<括弧外の乗除算<括弧内の加減算<括弧内の乗除算」になっている必要があります。
式を計算するときには、より括弧の内側の演算を優先して処理します。また、加減算よりも乗除算を優先するルールになっています。このため、式が正しく評価されるためには、優先順位が「括弧外の加減算<括弧外の乗除算<括弧内の加減算<括弧内の乗除算」になっている必要があります。
選択肢を見ると、まず「ウ」「エ」は明らかに誤りであるとわかります。なぜなら、11以下、12以下という範囲には0を含むからです。括弧内の優先度を高くするためには、括弧内での nest の値を括弧外よりも大きくしなければなりませんが、nest に加算される値が0だと、単に加減算は1、乗除算は2となり括弧内外の区別がつきません。 次に定数が1の場合を考えてみます。定数が1だと、括弧外の乗除算(優先度 2)と括弧内の加減算(優先度 1+1=2)が同じ優先度になってしまいます。〔プログラム(計算処理の部分)〕では、優先度が同じ演算が複数存在するときには左から順に実行するようになっているので、括弧内の加減算よりも括弧外の乗除算が優先されてしまい、正しい結果を得られません。
次に定数が1の場合を考えてみます。定数が1だと、括弧外の乗除算(優先度 2)と括弧内の加減算(優先度 1+1=2)が同じ優先度になってしまいます。〔プログラム(計算処理の部分)〕では、優先度が同じ演算が複数存在するときには左から順に実行するようになっているので、括弧内の加減算よりも括弧外の乗除算が優先されてしまい、正しい結果を得られません。 最後に定数が2の場合を考えています。定数が2であれば、括弧外の乗除算(優先度 2)よりも括弧内の加減算(優先度 2+1=3)の優先度が高くなるので、正しい演算順序が保証されます。
最後に定数が2の場合を考えています。定数が2であれば、括弧外の乗除算(優先度 2)よりも括弧内の加減算(優先度 2+1=3)の優先度が高くなるので、正しい演算順序が保証されます。 したがって、正しい演算順序が保証される定数の条件は 2以上 となります。
したがって、正しい演算順序が保証される定数の条件は 2以上 となります。
∴a=イ:2以上
〔bについて〕
priHigh と priLow に仮の値を割り当てて、選択肢ごとの下限値を用いた場合に、括弧外の演算の優先度と括弧内の演算の優先度の差がどのようになるかを考えます。
「ア」と「エ」で差がつかない priHigh=2、priLow=1 以外なら何でも良いのですが、ここでは priHigh=3、priLow=2 とします。
※例のように priHigh=3、priLow=2 の場合、2, 3, 4, 5 …、すなわち2以上が③④で加算される適切な値となります。「ア」の priHigh以上(3, 4, 5 …)は2を含まず、「イ」は priHigh+1以上(4, 5, 6 …)は2, 3を含まないので範囲として不適切です。
∴b=エ:priHigh-priLow+1以上
まずは、行③及び④の処理において定数の10を加減する対象となっている変数 nest の役割について考えてみましょう。nest は、行①及び②の処理において、Priority[] に格納される値のベースに使われています。Priority[]は、その名前(priority:優先度)が示すように演算の優先順位を保持する配列で、〔プログラム(計算処理の部分)〕ではこの値が大きい演算から先に順番する処理になっています。
行③では、式中に"("が見つかると nest に10を加えています。逆に行④では")"が見つかると10を引いています。つまり nest は、括弧の中の演算の優先度を高くするための変数であり、括弧の内部であるほど nest の値も大きくなります。

選択肢を見ると、まず「ウ」「エ」は明らかに誤りであるとわかります。なぜなら、11以下、12以下という範囲には0を含むからです。括弧内の優先度を高くするためには、括弧内での nest の値を括弧外よりも大きくしなければなりませんが、nest に加算される値が0だと、単に加減算は1、乗除算は2となり括弧内外の区別がつきません。



∴a=イ:2以上
〔bについて〕
priHigh と priLow に仮の値を割り当てて、選択肢ごとの下限値を用いた場合に、括弧外の演算の優先度と括弧内の演算の優先度の差がどのようになるかを考えます。
「ア」と「エ」で差がつかない priHigh=2、priLow=1 以外なら何でも良いのですが、ここでは priHigh=3、priLow=2 とします。
- priHigh=3 なので nest に加減する定数は3以上となり、その下限値は3になります。

- priHigh=3 なので nest に加減する定数は4以上となり、その下限値は4になります。

- priHigh=3、priLow=2 なので nest に加減する定数は1以上となり、その下限値は1になります。

- priHigh=3、priLow=2 なので nest に加減する定数は2以上となり、その下限値は2になります。

※例のように priHigh=3、priLow=2 の場合、2, 3, 4, 5 …、すなわち2以上が③④で加算される適切な値となります。「ア」の priHigh以上(3, 4, 5 …)は2を含まず、「イ」は priHigh+1以上(4, 5, 6 …)は2, 3を含まないので範囲として不適切です。
∴b=エ:priHigh-priLow+1以上
設問2
優先順位の等しい演算子が複数個含まれている整数式の,演算の実行順序について考察する。プログラムに関する次の記述中の に入れる正しい答えを,解答群の中から選べ。ここで,c1~c3に入れる答えは,cに関する解答群の中から組合せとして正しいものを選ぶものとする。
プログラム(計算処理の部分)では,優先順位の等しい演算子が複数個含まれている場合,演算を左から順に実行するようになっている。このプログラムでは,演算を左から順に実行するか右から順に実行するかは,行c1の内容がc2かc3かで決まる。
演算の実行順序によって,計算結果が異なることがある。例えば,次の四つの整数式のケースを考える。
プログラム(計算処理の部分)では,優先順位の等しい演算子が複数個含まれている場合,演算を左から順に実行するようになっている。このプログラムでは,演算を左から順に実行するか右から順に実行するかは,行c1の内容がc2かc3かで決まる。
演算の実行順序によって,計算結果が異なることがある。例えば,次の四つの整数式のケースを考える。
- ケース1:(12+3+1)×4×2
- ケース2:(12+3+1)÷4÷2
- ケース3:(12-3-1)×4×2
- ケース4:(12-3-1)÷4÷2
c に関する解答群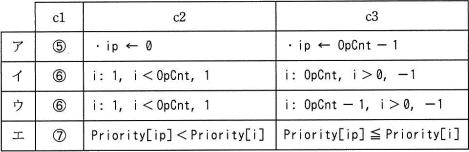

d に関する解答群
- 1
- 1及び2
- 1及び3
- 1及び4
解答選択欄
- c:
- d:
解答
- c=エ
- d=ア
解説
〔cについて〕
同じ優先順位(Priority[ip]=Priority[i])の演算が現れたとき、Priority[ip]<Priority[i] だと ip の値はそのままですが、Priority[ip]≦Priority[i] であれば ip は i の値で上書きされることになります。
例として、ip=1、i=2、Priority[1] と Priority[2] が等しい場合で考えてみると、
〔dについて〕
4つの式では、括弧内の加減算と、括弧が外れた後の乗除算が同じ優先順位になっているはずです。手間はかかりますが、実際に優先順位の同じ演算を左右両方から計算してみることで正しい答えを導きます。
【ケース1】
[左から演算]
(12+3+1)×4×2=(15+1)×4×2
=16×4×2=64×2
=128
[右から演算]
(12+3+1)×4×2=(12+4)×4×2
=16×4×2=16×8
=128
ケース1はどちらの結果も同じになります。
【ケース2】
[左から演算]
(12+3+1)÷4÷2=(15+1)÷4÷2
=16÷4÷2=4÷2
=2
[右から演算]
(12+3+1)÷4÷2=(12+4)÷4÷2
=16÷4÷2=16÷2
=8
ケース2は異なった結果になります。
【ケース3】
[左から演算]
(12-3-1)×4×2=(9-1)×4×2
=8×4×2=32×2
=64
[右から演算]
(12-3-1)×4×2=(12-2)×4×2
=10×4×2=10×8
=80
ケース3は異なった結果になります。
【ケース4】
[左から演算]
(12-3-1)÷4÷2=(9-1)÷4÷2
=8÷4÷2=2÷2
=1
[右から演算]
(12-3-1)÷4÷2=(12-2)÷4÷2
=10÷4÷2=10÷2
=5
ケース4は異なった結果になります。
以上より、【ケース1】のように式中に減算と除算を含まない場合に限り、左から実行しても右から実行しても計算結果が等しくなることがわかります。
∴d=ア:1
同じ優先順位(Priority[ip]=Priority[i])の演算が現れたとき、Priority[ip]<Priority[i] だと ip の値はそのままですが、Priority[ip]≦Priority[i] であれば ip は i の値で上書きされることになります。
例として、ip=1、i=2、Priority[1] と Priority[2] が等しい場合で考えてみると、
- Priority[1]<Priority[2] は偽
- ip=1 のまま。つまり優先順位の値が同じ場合、より左側に位置する演算が優先される
- Priority[1]≦Priority[2] は真
- ip=2 になる。つまり優先順位の値が同じ場合、より右側に位置する演算が優先される
〔dについて〕
4つの式では、括弧内の加減算と、括弧が外れた後の乗除算が同じ優先順位になっているはずです。手間はかかりますが、実際に優先順位の同じ演算を左右両方から計算してみることで正しい答えを導きます。
【ケース1】
[左から演算]
(12+3+1)×4×2=(15+1)×4×2
=16×4×2=64×2
=128
[右から演算]
(12+3+1)×4×2=(12+4)×4×2
=16×4×2=16×8
=128
ケース1はどちらの結果も同じになります。
【ケース2】
[左から演算]
(12+3+1)÷4÷2=(15+1)÷4÷2
=16÷4÷2=4÷2
=2
[右から演算]
(12+3+1)÷4÷2=(12+4)÷4÷2
=16÷4÷2=16÷2
=8
ケース2は異なった結果になります。
【ケース3】
[左から演算]
(12-3-1)×4×2=(9-1)×4×2
=8×4×2=32×2
=64
[右から演算]
(12-3-1)×4×2=(12-2)×4×2
=10×4×2=10×8
=80
ケース3は異なった結果になります。
【ケース4】
[左から演算]
(12-3-1)÷4÷2=(9-1)÷4÷2
=8÷4÷2=2÷2
=1
[右から演算]
(12-3-1)÷4÷2=(12-2)÷4÷2
=10÷4÷2=10÷2
=5
ケース4は異なった結果になります。
以上より、【ケース1】のように式中に減算と除算を含まない場合に限り、左から実行しても右から実行しても計算結果が等しくなることがわかります。
∴d=ア:1
設問3
プログラムの動作に関する次の記述中の に入れる正しい答えを,解答群の中から選べ。
符号付き整定数(数字の並びの先頭に符号+又は-を付けた定数)を含む整数式を考える。符号付き整定数は,例2のように括弧で囲んで記述する。ただし,符号付き整定数の直前の文字が演算子でない場合は,例3のように括弧で囲まなくてもよい。
このように,符号付き整定数を含む整数式を受け取ったとき,プログラムはe。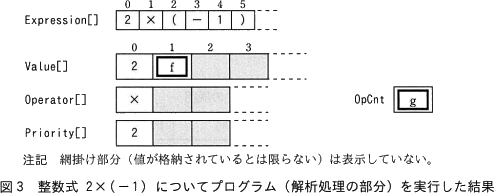
符号付き整定数(数字の並びの先頭に符号+又は-を付けた定数)を含む整数式を考える。符号付き整定数は,例2のように括弧で囲んで記述する。ただし,符号付き整定数の直前の文字が演算子でない場合は,例3のように括弧で囲まなくてもよい。
- 例2: (+2)×((-3)+(-4))
- 例3: +2×(-3+(-4))
このように,符号付き整定数を含む整数式を受け取ったとき,プログラムはe。

e に関する解答群
- 整数式が符号付き整定数で始まる場合に,正しい値を返さない
- 整数式中に符号 - の付いた符号付き整定数がある場合に,正しい値を返さない
- 整数式中に二つ以上の符号付き整定数が含まれる場合に,正しい値を返さない
- 正しい値を返す
f,g に関する解答群
- -1
- 0
- 1
- 2
解答選択欄
- e:
- f:
- g:
解答
- e=エ
- f=イ
- g=エ
解説
処理は、解析部分→計算部分と進むので、先にf,gから解説していきます。
式 2×(-1) の解析部分の処理をトレースすると次のようになります。
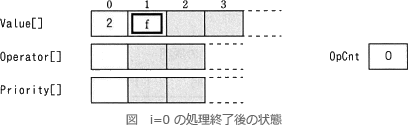
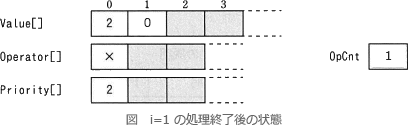
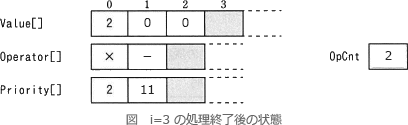
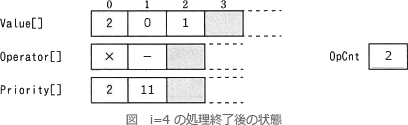
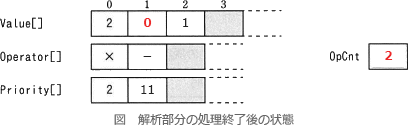 したがって、解析部分の処理が終わるとfには0が、gには2が格納されています。
したがって、解析部分の処理が終わるとfには0が、gには2が格納されています。
∴f=イ:0
g=エ:2
〔eについて〕
計算部分の処理では、まず優先順位の高い"-"の演算が選択され、Value[1]-Value[2](すなわち、0-1)の実行結果が Value[1] に格納されます。
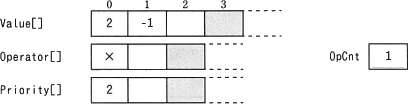 そして、残った"×"の演算が選択され、Value[0]×Value[1](すなわち、2×(-1))の実行結果が Value[0] に格納されます。
そして、残った"×"の演算が選択され、Value[0]×Value[1](すなわち、2×(-1))の実行結果が Value[0] に格納されます。
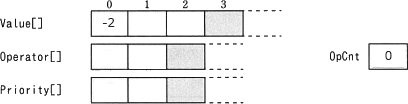 このように、符号付き整定数を含む場合であっても Value[] に0を挟むことによって、正しい結果が返るようになっています。
このように、符号付き整定数を含む場合であっても Value[] に0を挟むことによって、正しい結果が返るようになっています。
∴e=エ:正しい値を返す
最後に、本問のアルゴリズムをJavaScriptで実装したものを掲載します。動作の確認などにご使用ください。
式 2×(-1) の解析部分の処理をトレースすると次のようになります。
OPCnt ← 0, Value[0] ← 0, nest ← 0
//以下、iが0から5まで繰り返す
//i = 0 の処理
chr ← 2
Value[0] ← 10×0+2 //Value[0] = 2
//以下、iが0から5まで繰り返す
//i = 0 の処理
chr ← 2
Value[0] ← 10×0+2 //Value[0] = 2

//i = 1 の処理
chr ← ×
Operator[0] ← ×
Priority[0] ← 0+2 //Priority[0] = 2
OpCnt ← 0+1 //OpCnt = 1
Value[1] ← 0
chr ← ×
Operator[0] ← ×
Priority[0] ← 0+2 //Priority[0] = 2
OpCnt ← 0+1 //OpCnt = 1
Value[1] ← 0

//i = 2 の処理
chr ← (
nest ← 0+10 //nest = 10
chr ← (
nest ← 0+10 //nest = 10
//i = 3 の処理
chr ← -
Operator[1] ← -
Priority[1] ← 10+1 //Priority[1] = 11
OpCnt ← 1+1 //OpCnt = 2
Value[2] ← 0
chr ← -
Operator[1] ← -
Priority[1] ← 10+1 //Priority[1] = 11
OpCnt ← 1+1 //OpCnt = 2
Value[2] ← 0

//i = 4 の処理
chr ← 1
Value[2] ← 10×0+1 //Value[2] = 1
chr ← 1
Value[2] ← 10×0+1 //Value[2] = 1

//i = 5 の処理
chr ← )
nest ← 10-10 //nest = 0
chr ← )
nest ← 10-10 //nest = 0

∴f=イ:0
g=エ:2
〔eについて〕
計算部分の処理では、まず優先順位の高い"-"の演算が選択され、Value[1]-Value[2](すなわち、0-1)の実行結果が Value[1] に格納されます。
Value[1] ← 0-1

Value[0] ← 2×-1

∴e=エ:正しい値を返す
最後に、本問のアルゴリズムをJavaScriptで実装したものを掲載します。動作の確認などにご使用ください。
