HOME»基本情報技術者平成27年秋期問題»午後問2
基本情報技術者過去問題 平成27年秋期 午後問2
⇄問題文と設問を画面2分割で開く⇱問題PDF問2 ハードウェア
浮動小数点数に関する次の記述を読んで，設問1～4に答えよ。
α＝0，又は1≦|α|＜2を満たすα，及び－126≦β≦127を満たすβを用いて α×2β の形で表記される浮動小数点数を，図1に示す32ビット単精度浮動小数点形式の表現(以下，単精度表現という)で近似する。
α＝0，又は1≦|α|＜2を満たすα，及び－126≦β≦127を満たすβを用いて α×2β の形で表記される浮動小数点数を，図1に示す32ビット単精度浮動小数点形式の表現(以下，単精度表現という)で近似する。
- 符号部(ビット番号31)
αの値が正のとき 0，負のとき 1 が入る。 - 指数部(ビット番号30～23)
βの値に127を加えた値が2進数で入る。 - 仮数部(ビット番号22～0)
|α|の整数部分 1 を省略し，残りの小数部分が，ビット番号 22 に小数第1位が来るような2進数で入る。このとき，仮数部に格納できない部分については切り捨てる。 - αの値が0の場合，符号部，指数部，仮数部ともに 0 とする。
設問1
0.625 を単精度表現したときに指数部に入る値として正しい答えを，解答群の中から選べ。
解答群
- (00)16
- (7E)16
- (7F)16
- (FE)16
- (FF)16
解答選択欄
解答
- イ
解説
0.625は0.5＋0.125なので2進数表記では (0.101)2 です。仮数部 0.101 の最上位ビットが整数1けた目にくるように正規化すると、1.01×2-1になります
[符号部]
正の値なので 0
[指数部]
指数部＝β＋127 なので
指数部＝－1＋127＝126
＝(01111110)2＝(7E)16
[仮数部]
0100…00
∴イ：(7E)16
[符号部]
正の値なので 0
[指数部]
指数部＝β＋127 なので
指数部＝－1＋127＝126
＝(01111110)2＝(7E)16
[仮数部]
0100…00
∴イ：(7E)16
設問2
次の単精度表現された数値として正しい答えを，解答群の中から選べ。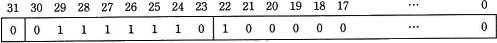
解答群
- 0.125
- 0.25
- 0.375
- 0.5
- 0.75
- 1.5
解答選択欄
解答
- オ
解説
[符号部]
0（正数）
[指数部]
(0111110)2
＝26＋25＋24＋23＋22＋21
＝64＋32＋16＋8＋4＋2
＝126
β＝126－127＝－1
[仮数部]
10…00 なので、整数部分の1を加えて 1.1
これらを組み合わせると、この単精度表現が示す浮動小数点数は「1.1×2-1」とわかります。
1.1×2-1＝(0.11)
＝2-1＋2-2＝0.5＋0.25
＝0.75
∴オ：0.75
0（正数）
[指数部]
(0111110)2
＝26＋25＋24＋23＋22＋21
＝64＋32＋16＋8＋4＋2
＝126
β＝126－127＝－1
[仮数部]
10…00 なので、整数部分の1を加えて 1.1
これらを組み合わせると、この単精度表現が示す浮動小数点数は「1.1×2-1」とわかります。
1.1×2-1＝(0.11)
＝2-1＋2-2＝0.5＋0.25
＝0.75
∴オ：0.75
設問3
次の記述中の に入れる正しい答えを，解答群の中から選べ。
二つの浮動小数点数AとBの加算を行う。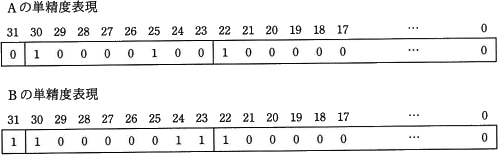
AとBの加算を，次の①，②の手順で行う。
二つの浮動小数点数AとBの加算を行う。
- 指数部の値を大きい方に合わせる。Aが(1.1)2×25であることから，Bを(－(a)2)×25とする。
- 加算を行う。
((1.1)2＋(－(a)2))×25＝(1.1)2×2b
a に関する解答群
- 0.001
- 0.01
- 0.011
- 0.1
- 0.11
- 1.1
b に関する解答群
- 3
- 4
- 5
- 6
- 130
- 131
- 132
解答選択欄
- a:
- b:
解答
- a=オ
- b=イ
解説
〔aについて〕
[符号部]
1（負数）
[指数部]
(10000011)2
＝27＋21＋20
＝128＋2＋1
＝131
β＝131－127＝4
[仮数部]
10…00 なので、整数部分の1を加えて 1.1
これらを組み合わせると、Bの単精度表現が示す浮動小数点数は「－1.1×24」とわかります。
さらに①の計算の過程で指数部をAと同じ 25 に合わせているので、
－1.1×24＝－0.11×25
∴a＝オ：0.11
〔bについて〕
AとBの加算を行うと次のようになります。
1.1×25＋(－0.11×25)
＝(1.1－0.11)×25
＝0.11×25
＝1.1×24
∴b＝イ：4
1（負数）
[指数部]
(10000011)2
＝27＋21＋20
＝128＋2＋1
＝131
β＝131－127＝4
[仮数部]
10…00 なので、整数部分の1を加えて 1.1
これらを組み合わせると、Bの単精度表現が示す浮動小数点数は「－1.1×24」とわかります。
さらに①の計算の過程で指数部をAと同じ 25 に合わせているので、
－1.1×24＝－0.11×25
∴a＝オ：0.11
〔bについて〕
AとBの加算を行うと次のようになります。
1.1×25＋(－0.11×25)
＝(1.1－0.11)×25
＝0.11×25
＝1.1×24
∴b＝イ：4
設問4
次の記述中の に入れる正しい答えを，解答群の中から選べ。
設問3のAについてA×10の値は，次の①～③の手順で求めることができる。
設問3のAについてA×10の値は，次の①～③の手順で求めることができる。
- A×8の値を求める。
A×8＝(1.1)2×25×8＝(1.1)2×25×23＝(1.1)2×28 - A×2の値を同様に求める。
- ①と②の結果を加算する。
c に関する解答群
解答選択欄
- c:
解答
- c=ウ
解説
〔cについて〕
②のA×2の値を①の方法と同様に計算します。
1.1×25×21＝1.1×26
次にA×8の計算結果である「1.1×28」と上記の「1.1×26」を設問3の方法で加算します。
まず、先程と同様に 1.1×26 の指数部の値を大きいほうの 28 に揃えます。
1.1×26＝0.011×28
加算を行います。
1.1×28＋0.011×28
＝(1.1＋0.011)×28
＝1.111×28
最後に計算結果を単精度表現に直します。
[符号部]
0（正数）
[指数部]
8＋127＝135
＝(10000111)2
[仮数部]
11100…00
したがって「ウ」が適切です。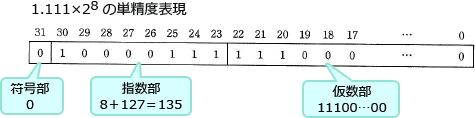
②のA×2の値を①の方法と同様に計算します。
1.1×25×21＝1.1×26
次にA×8の計算結果である「1.1×28」と上記の「1.1×26」を設問3の方法で加算します。
まず、先程と同様に 1.1×26 の指数部の値を大きいほうの 28 に揃えます。
1.1×26＝0.011×28
加算を行います。
1.1×28＋0.011×28
＝(1.1＋0.011)×28
＝1.111×28
最後に計算結果を単精度表現に直します。
[符号部]
0（正数）
[指数部]
8＋127＝135
＝(10000111)2
[仮数部]
11100…00
したがって「ウ」が適切です。