HOME»基本情報技術者平成24年春期問題»午後問2
基本情報技術者過去問題 平成24年春期 午後問2
⇄問題文と設問を画面2分割で開く⇱問題PDF問2 ソフトウェア
コンパイラの最適化に関する次の記述を読んで,設問1~3に答えよ。
コンパイラとは,プログラム言語で記述された原始プログラムを翻訳して目的プログラムを生成するためのソフトウェアである。コンパイラの機能の一つに最適化がある。最適化では,原始プログラムを翻訳する過程で,プログラムの実行時間を短くするために原始プログラムの構造を変換する。最適化の方法の例を表1に示す。 擬似言語の形式で記述したプログラムの一部(以下,プログラム1という)に対して,表1の最適化の方法を複数組み合わせて最適化した例を,表2に示す。
擬似言語の形式で記述したプログラムの一部(以下,プログラム1という)に対して,表1の最適化の方法を複数組み合わせて最適化した例を,表2に示す。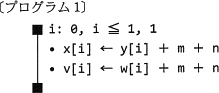
コンパイラとは,プログラム言語で記述された原始プログラムを翻訳して目的プログラムを生成するためのソフトウェアである。コンパイラの機能の一つに最適化がある。最適化では,原始プログラムを翻訳する過程で,プログラムの実行時間を短くするために原始プログラムの構造を変換する。最適化の方法の例を表1に示す。

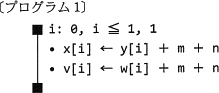

設問1
次の記述中の に入れる正しい答えを,解答群の中から選べ。
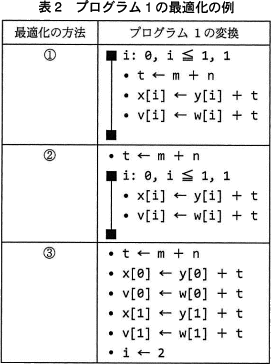
表2において,最適化の方法を①,②,③の順で適用するとき,②で適用される最適化の方法はaであり,③で適用される最適化の方法はbである。
表2において,最適化の方法を①,②,③の順で適用するとき,②で適用される最適化の方法はaであり,③で適用される最適化の方法はbである。
a,b に関する解答群
- 関数のインライン展開
- 共通部分式の削除
- 定数の畳込み
- 定数伝播
- 無用命令の削除
- ループ内不変式の移動
- ループのアンローリング
解答選択欄
- a:
- b:
解答
- a=カ
- b=キ
解説
〔aについて〕
①から②への変化はループ内にあった「t ← m + n」の式がループ外に移動していることです。したがって、「ループ内不変式の移動」が適切です。
mとnはループ内で変更されることがない変数のため、ループ中はtの値も一定です。よって、t を計算する式をループ外に出すことでループの度に t を計算する無駄を省くことができます。
∴a=カ:ループ内不変式の移動
〔bについて〕
②から③への変化はループ処理がなくなり、ループ中に行われるi=0,i=1の時の処理が4つの順次処理に展開されていることです。したがって、「ループのアンローリング」が適切です。
∴b=キ:ループのアンローリング
①から②への変化はループ内にあった「t ← m + n」の式がループ外に移動していることです。したがって、「ループ内不変式の移動」が適切です。
mとnはループ内で変更されることがない変数のため、ループ中はtの値も一定です。よって、t を計算する式をループ外に出すことでループの度に t を計算する無駄を省くことができます。
∴a=カ:ループ内不変式の移動
〔bについて〕
②から③への変化はループ処理がなくなり、ループ中に行われるi=0,i=1の時の処理が4つの順次処理に展開されていることです。したがって、「ループのアンローリング」が適切です。
∴b=キ:ループのアンローリング
設問2
次の記述中の に入れる正しい答えを,解答群の中から選べ。
関数のインライン展開の例を図1に示す。図1の関数 func をインライン展開した場合,実引数 10 の値が仮引数 p に代入され,その値 10 が関数 func 内の変数 p の値になる(図1①)。次に,cの方法を適用することによって,条件式 p≧10 の判定結果や p を含んだ計算式の計算結果がコンパイル時に確定する(図1②)。その結果,func(10)を値 15 に置き換えることができる(図1③)。
なお,#w はコンパイラが最適化をしたときに生成した整数型の変数である。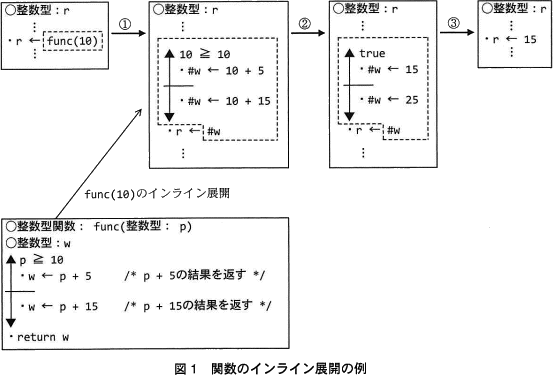
関数のインライン展開の例を図1に示す。図1の関数 func をインライン展開した場合,実引数 10 の値が仮引数 p に代入され,その値 10 が関数 func 内の変数 p の値になる(図1①)。次に,cの方法を適用することによって,条件式 p≧10 の判定結果や p を含んだ計算式の計算結果がコンパイル時に確定する(図1②)。その結果,func(10)を値 15 に置き換えることができる(図1③)。
なお,#w はコンパイラが最適化をしたときに生成した整数型の変数である。

c に関する解答群
- 共通部分式の削除
- 定数の畳込み
- 定数伝播
- 無用命令の削除
- ループ内不変式の移動
- ループのアンローリング
解答選択欄
- c:
解答
- c=イ
解説
図1②がcの処理にあたります。cが適用されることによるプログラムの変化部分は、以下の3点です。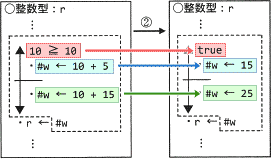 これら3つの変化は命令文中の数値(定数)同士の計算式・比較式が、その結果で置き換えられたことによるものです。
これら3つの変化は命令文中の数値(定数)同士の計算式・比較式が、その結果で置き換えられたことによるものです。
表1「最適化の方法の例」より、同様の方法を探すと「定数同士の計算式を,その結果で置き換える」操作を行う定数の畳込みに該当することがわかります。
∴c=イ:定数の畳込み
- 10≧10 ⇒ true //常に真
- #w ← 10 + 5 ⇒ #w ← 15
- #w ← 10 + 15 ⇒ #w ← 25

表1「最適化の方法の例」より、同様の方法を探すと「定数同士の計算式を,その結果で置き換える」操作を行う定数の畳込みに該当することがわかります。
∴c=イ:定数の畳込み
設問3
次の記述中の に入れる適切な答えを,解答群の中から選べ。
最適化をしないときと最適化をしたときとで浮動小数点数の演算の結果が異なる場合がある。プログラム1に対して表2の最適化をしなかったものと,最適化をしたものとに,y[0]=307000000.0,y[1]=305000000.0,m=-303000000.0,n=4.0 を与えて実行した。その結果の x[0],X[1] が次のとおりになった。ここで,同一優先順位の算術演算子は,左から順に演算する。
最適化をしないときと最適化をしたときとで浮動小数点数の演算の結果が異なる場合がある。プログラム1に対して表2の最適化をしなかったものと,最適化をしたものとに,y[0]=307000000.0,y[1]=305000000.0,m=-303000000.0,n=4.0 を与えて実行した。その結果の x[0],X[1] が次のとおりになった。ここで,同一優先順位の算術演算子は,左から順に演算する。
- 最適化をしないとき: x[0]=4000004.0,x[1]=2000004.0
- 最適化をしたとき: x[0]=4000000.0,x[1]=2000000.0
d に関する解答群
- 関数のインライン展開
- 共通部分式の削除
- 定数の畳込み
- 定数伝播
- 無用命令の削除
- ループ内不変式の移動
- ループのアンローリング
e に関する解答群
- 桁あふれ
- 桁落ち
- 情報落ち
- 丸め誤差
解答選択欄
- d:
- e:
解答
- d=イ
- e=ウ
解説
〔dについて〕
まず"最適化なし"と"最適化あり"で x[0] が計算される手順について考えてみます。「同一優先順位の算術演算子は,左から順に演算する」ことに注意します。
[最適化なし]
x[0] ← y[0] + m + n
t ← m + n
x[0] ← y[0] + t
これは、ループ中で何度も使用する「m+n」の演算を予め変数tに計算し、「m+n」を t で置き換えた影響によるものです。
表1「最適化方法の例」より、この操作に該当する方法を探すと共通部分式の削除にであることがわかります。
∴d=イ:共通部分式の削除
〔eについて〕
選択肢の4つの計算誤差については以下の通りです。
実際に -303000000.0+4.0 の浮動小数点計算を行うと以下のように4.0を表すビット列が有効桁数外になり、計算結果に反映されないことが確認できます。 ∴e=ウ:情報落ち
∴e=ウ:情報落ち
まず"最適化なし"と"最適化あり"で x[0] が計算される手順について考えてみます。「同一優先順位の算術演算子は,左から順に演算する」ことに注意します。
[最適化なし]
x[0] ← y[0] + m + n
- y[0] + m を計算する
- 1の結果にnを加える
- 2の結果をx[0]に格納する
t ← m + n
x[0] ← y[0] + t
- m + n の結果を t に格納する
- y[0]に t を加える
- 2の結果をx[0]に格納する
これは、ループ中で何度も使用する「m+n」の演算を予め変数tに計算し、「m+n」を t で置き換えた影響によるものです。
表1「最適化方法の例」より、この操作に該当する方法を探すと共通部分式の削除にであることがわかります。
∴d=イ:共通部分式の削除
〔eについて〕
選択肢の4つの計算誤差については以下の通りです。
- 桁あふれ(算術オーバーフロー)
- 数値演算の結果が、プログラムで使用している数値型変数の型の最大・最小値や、データ領域の上限よりも大きくなること。誤った計算結果が格納されたり、本来計算結果を格納するべきでない位置にデータが書き込まれたりする不具合が生じる。
- 桁落ち
- 浮動小数点演算において、符号が等しく絶対値の非常に近い値同士の減算や、符号が逆で絶対値の非常に近い値同士の加算をした場合に、有効桁数が減ってしまうことで生じる誤差
- 情報落ち
- 浮動小数点演算において,絶対値の大きな数と絶対値の小さな数の加減算を行ったとき,絶対値の小さな数の有効けたの一部又は全部が結果に反映されないことで生じる誤差
- 丸め誤差
- 計算の過程で、四捨五入や切り捨て・切り上げなどを行うことによって生じる誤差
実際に -303000000.0+4.0 の浮動小数点計算を行うと以下のように4.0を表すビット列が有効桁数外になり、計算結果に反映されないことが確認できます。

