HOME»基本情報技術者平成24年春期問題»午後問7
基本情報技術者過去問題 平成24年春期 午後問7
⇄問題文と設問を画面2分割で開く⇱問題PDF問7 経営・関連法規
正味現在価値(Net Present Value)による投資採算性の評価に関する次の記述を読んで，設問1～3に答えよ。
日用品メーカーのD社では，業務効率の向上及び 2016 年に予定されている新生産設備の稼働への対応を目的として，新たに生産管理システムの導入を検討している。生産管理システムの導入における投資採算性の評価を，企画課で行うことになった。企画課で試算したシステム導入に掛かる投資と効果は次のとおりである。
なお，NPVの計算では，利子率を割引率と呼ぶこともある。
日用品メーカーのD社では，業務効率の向上及び 2016 年に予定されている新生産設備の稼働への対応を目的として，新たに生産管理システムの導入を検討している。生産管理システムの導入における投資採算性の評価を，企画課で行うことになった。企画課で試算したシステム導入に掛かる投資と効果は次のとおりである。
- 投資
生産管理システムの導入の方法として，次の2案を検討した。- 業務効率向上のための投資と新生産設備の稼働対応の投資の両方を 2012 年に行う(以下，一括投資という)場合，7億5千万円が必要となる。
- 業務効率向上のための投資を 2012 年に，新生産設備の稼働対応の投資を 2015 年に行う(以下，分割投資という)場合，2012 年に 5 億円，2015 年に 3 億円が必要となる。
- 効果
(1)のどちらの場合でも，生産管理システムの導入によって，2013 年からは年間 2 億円，2016 年からは年間 3 億円のコスト削減が見込まれる。
なお，NPVの計算では，利子率を割引率と呼ぶこともある。
設問1
NPVを使った投資課算性の評価に関する次の記述中の に入れる正しい答えを，解答群の中から選べ。
NPVを計算するときは，各年に増減するキャッシュの現在価値を計算する必要がある。割引率を r で複利計算し，n 年後のキャッシュを C と表すとき，その現在価値は，aと表せる。
なお，投資年については，n＝0で計算する。
将来の各年におけるキャッシュの増減に対して，その現在価値を計算し，次に各年の現在価値を合計することでNPVが求められる。NPVが正のときは，その投資案は採算性があり，NPVが大きいほど採算性が高いと評価される。NPVが負のときは，その投資案は採算性がなく，投資するべきでないと評価される。NPVが正の投資案が二つ以上あるときは，NPVの最も大きな投資案を選択するべきである。
NPVを計算するときは，各年に増減するキャッシュの現在価値を計算する必要がある。割引率を r で複利計算し，n 年後のキャッシュを C と表すとき，その現在価値は，aと表せる。
なお，投資年については，n＝0で計算する。
将来の各年におけるキャッシュの増減に対して，その現在価値を計算し，次に各年の現在価値を合計することでNPVが求められる。NPVが正のときは，その投資案は採算性があり，NPVが大きいほど採算性が高いと評価される。NPVが負のときは，その投資案は採算性がなく，投資するべきでないと評価される。NPVが正の投資案が二つ以上あるときは，NPVの最も大きな投資案を選択するべきである。
a に関する解答群
解答選択欄
- a:
解答
- a=ア
解説
〔aについて〕
利子率0.05で100万を預金すると年ごとの金額は以下のように増加していきます。
[1年後] 100×1.05＝105(万円)
[2年後] 100×1.05×1.05＝110.25(万円)
[3年後] 100×1.05×1.05×1.05≒115.8(万円)
この例を基に考えると、現在の金額に利子率rの複利が付いた場合のn年後の金額は、以下の式で計算ができます。
現在の金額×(1＋r)n＝n年後の金額
上の例とは逆に利子率とn年後の金額がわかれば、この式を使って現在の金額を導くことも可能です。n年後の金額に「n年後のキャッシュ(C)」、現在の金額に「現在価値」を当てはめると、
現在価値×(1＋r)n＝C
という関係式になり、これを現在価値について解くと、
現在価値＝C／(1＋r)n
という「ア」の式になります。
∴a＝ア: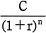
これとは別に選択肢の各式に設問の例にある C=100，r=0.05，n=2 を代入して現在価値 約91万円が正しく求まるかで正解を導くこともできます。
利子率0.05で100万を預金すると年ごとの金額は以下のように増加していきます。
[1年後] 100×1.05＝105(万円)
[2年後] 100×1.05×1.05＝110.25(万円)
[3年後] 100×1.05×1.05×1.05≒115.8(万円)
この例を基に考えると、現在の金額に利子率rの複利が付いた場合のn年後の金額は、以下の式で計算ができます。
現在の金額×(1＋r)n＝n年後の金額
上の例とは逆に利子率とn年後の金額がわかれば、この式を使って現在の金額を導くことも可能です。n年後の金額に「n年後のキャッシュ(C)」、現在の金額に「現在価値」を当てはめると、
現在価値×(1＋r)n＝C
という関係式になり、これを現在価値について解くと、
現在価値＝C／(1＋r)n
という「ア」の式になります。
∴a＝ア:
これとは別に選択肢の各式に設問の例にある C=100，r=0.05，n=2 を代入して現在価値 約91万円が正しく求まるかで正解を導くこともできます。
- 100／(1＋0.05)2
＝100／1.1025＝90.702…≒91 - 100／(1－0.05)2
＝100／0.9025＝110.80… - 100／0.052
＝100／0.0025＝40000 - 100×(1＋0.05)2
＝100×1.1025＝110.25 - 100×(1－0.05)2
＝100×0.9025＝90.25 - 100×0.052
＝100×0.0025＝0.25
設問2
生産管理システムの投資採算性の評価に関する次の記述中の に入れる適切な答えを，解答群の中から選べ。
企画課では，次の手順で生産管理システム導入の投資採算性の評価を行うことにした。一括投資する場合の生産管理システム導入のNPVを 計算する表1と，分割投資する場合のNPVを計算する表2を作成した。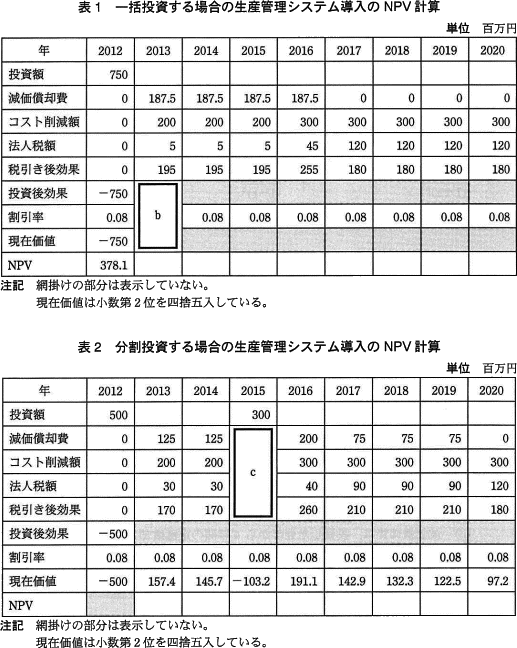
企画課では，表1と表2の結果からdと判断した。
企画課では，次の手順で生産管理システム導入の投資採算性の評価を行うことにした。一括投資する場合の生産管理システム導入のNPVを 計算する表1と，分割投資する場合のNPVを計算する表2を作成した。
- 2012 年から 2020 年までの期間を対象にNPVを計算する。
- 各年のコスト削減額から減価償却費を差し引いて，各年の課税対象効果を求める。
- 減価償却費は，投資した翌年から4年間の定額償却(残存価額は0円)として求める。
- 法人税率を 40% とし，各年の課税対象効果から法人税として控除される法人税額を求める。
- 各年のコスト削減額から法人税額を差し引いて税引き後効果を求め，更に税引き後効果から各年の投資額を差し引いて各年の投資後効果(キャッシュ増減額)を求める。
- 割引率を 0.08 とし，各年の投資後効果の現在価値を計算する。
- (6)で計算した各年の現在価値を合計し，投資案のNPVを計算する。
b に関する解答群
c に関する解答群
d に関する解答群
- 一括投資，分割投資のどちらの投資案にしてもよい
- 一括投資，分割投資のどちらの投資案もするべきでない
- 一括投資するべきである
- 分割投資するべきである
解答選択欄
- b:
- c:
- d:
解答
- b=カ
- c=ア
- d=エ
解説
〔bについて〕
計算対象は、2013年度の投資後効果、割引率、現在価値です。
まず投資後効果は、税引き後効果から各年の投資額を差し引いて求めます。表1より2013年の税引き後効果は195、投資額は0なので、2013年の投資後効果は、
195－0＝195(百万円)
次に割引率ですが、設問中に「割引率は0.08として現在価値を計算する」とあるので割引率の項目には0.08が入ります。
最後に2013年のキャッシュの現在価値を設問1で導いたを用いて計算します。投資後効果 195、割引率 0.08、投資年度からの経過年数(n) 1 なので、
195／(1＋0.08)1
＝195／1.08
＝180.55…≒180.6
したがってbには「カ」の数値の組合せが入ります。
∴b＝カ
〔cについて〕
計算対象は、2015年度の減価償却費、コスト削減額、法人税額、税引き後効果です。
まず減価償却費ですが、「減価償却費は投資した翌年から4年間の定額償却」です。2015年は、初年度に投資された500百万円の3回目の償却年にあたるため、前年(2014年)と同様に500百万円を4分割した125百万円が計上されます。2015年に投資した分は2016年からの償却開始となるため、2015年には減価償却費が発生しないことに注意しましょう。
コスト削減額は、一括投資、分割投資のどちらの案でも2013～2015年は年間2億、2016年からは3億円なので、2015年のコスト削減効果は2億円(200百万円)が適切です。
法人税額は「課税対象効果×0.4」で計算できます。課税対象効果は「コスト削減額－減価償却費」の結果なので、
(200－125)×0.4＝30(百万円)
最後に「コスト削減額－法人税額」を計算し税引き後効果を求めます。
200－30＝170(百万円)
したがってcには「ア」の数値の組合せが入ります。
∴c＝ア
〔dについて〕
表1ではNPVが378.1百万円と計算されていますが、表2では隠されているため現在価値を合計してNPVを算出します。
－500＋157.4＋145.7－103.2＋191.1+142.9＋132.3＋122.5＋97.2
＝385.9(百万円)
両案のNPVを比較すると「一括投資(378.1)＜分割投資(385.9)」であるため、よりNPVの高い分割投資の方が有利と判断できます。
∴d＝エ：分割投資するべきである
計算対象は、2013年度の投資後効果、割引率、現在価値です。
まず投資後効果は、税引き後効果から各年の投資額を差し引いて求めます。表1より2013年の税引き後効果は195、投資額は0なので、2013年の投資後効果は、
195－0＝195(百万円)
次に割引率ですが、設問中に「割引率は0.08として現在価値を計算する」とあるので割引率の項目には0.08が入ります。
最後に2013年のキャッシュの現在価値を設問1で導いた
を用いて計算します。投資後効果 195、割引率 0.08、投資年度からの経過年数(n) 1 なので、195／(1＋0.08)1
＝195／1.08
＝180.55…≒180.6
したがってbには「カ」の数値の組合せが入ります。
∴b＝カ
〔cについて〕
計算対象は、2015年度の減価償却費、コスト削減額、法人税額、税引き後効果です。
まず減価償却費ですが、「減価償却費は投資した翌年から4年間の定額償却」です。2015年は、初年度に投資された500百万円の3回目の償却年にあたるため、前年(2014年)と同様に500百万円を4分割した125百万円が計上されます。2015年に投資した分は2016年からの償却開始となるため、2015年には減価償却費が発生しないことに注意しましょう。
コスト削減額は、一括投資、分割投資のどちらの案でも2013～2015年は年間2億、2016年からは3億円なので、2015年のコスト削減効果は2億円(200百万円)が適切です。
法人税額は「課税対象効果×0.4」で計算できます。課税対象効果は「コスト削減額－減価償却費」の結果なので、
(200－125)×0.4＝30(百万円)
最後に「コスト削減額－法人税額」を計算し税引き後効果を求めます。
200－30＝170(百万円)
したがってcには「ア」の数値の組合せが入ります。
∴c＝ア
〔dについて〕
表1ではNPVが378.1百万円と計算されていますが、表2では隠されているため現在価値を合計してNPVを算出します。
－500＋157.4＋145.7－103.2＋191.1+142.9＋132.3＋122.5＋97.2
＝385.9(百万円)
両案のNPVを比較すると「一括投資(378.1)＜分割投資(385.9)」であるため、よりNPVの高い分割投資の方が有利と判断できます。
∴d＝エ：分割投資するべきである
設問3
生産管理システムのNPVの再計算に関する次の記述中の に入れる適切な答えを，解答群の中から選べ。
なお，解答は重複して選んでもよい。
企画課で作成した表1，表2を社内の関係部署に説明したところ，生産課から，生産管理システムに新たな機能を追加したいとの要望があった。新たな機能の追加には，2012 年に5千万円の追加投資が必要となる。その場合，生産管理システムの機能が向上し，追加効果は年間で5百万円の見込みである。
機能を追加した場合のNPVを企画課で計算した結果，一括投資の場合のNPVは3億6,190万円，分割投資の場合のNPVは3億7,000万円であった。企画課では，これらの結果と表1，表2から，生産課の要望については，eと判断した。
また，経理課から，D社では情報システムの減価償却期間を4年間ではなく5年間で 行っているので，表1，表2もそのように修正するべきであるとのコメントがあった。減価償却期間を5年に変更すると，表1の各年の減価償却費は表3のように変わる。
表3によると，2013 年から 2016 年までの各年の減価償却費は表1に比べて下がり，2017 年の減価償却費は表1に比べて上がり，2018 年以降の減価償却費は 表1と同じであることが分かる。したがって，2013 年から 2016 年までの税引き後効果はfことになり，2017 年の税引き後効果はgことになる。2020 年までの減価償却費の総額は変わらないものの，現在価値の考え方を考慮すると，NPVはhと考えられる。これは，表2についても同様である。
企画課では，経理課のコメントに従って表1と表2を修正して，再度投資採算性を評価した。
なお，解答は重複して選んでもよい。
企画課で作成した表1，表2を社内の関係部署に説明したところ，生産課から，生産管理システムに新たな機能を追加したいとの要望があった。新たな機能の追加には，2012 年に5千万円の追加投資が必要となる。その場合，生産管理システムの機能が向上し，追加効果は年間で5百万円の見込みである。
機能を追加した場合のNPVを企画課で計算した結果，一括投資の場合のNPVは3億6,190万円，分割投資の場合のNPVは3億7,000万円であった。企画課では，これらの結果と表1，表2から，生産課の要望については，eと判断した。
また，経理課から，D社では情報システムの減価償却期間を4年間ではなく5年間で 行っているので，表1，表2もそのように修正するべきであるとのコメントがあった。減価償却期間を5年に変更すると，表1の各年の減価償却費は表3のように変わる。
企画課では，経理課のコメントに従って表1と表2を修正して，再度投資採算性を評価した。
e に関する解答群
- 一括投資，分割投資のどちらの場合も受け入れるべきではない
- 一括投資，分割投資のどちらの場合も受け入れるべきである
- 一括投資の場合だけ受け入れるべきである
- 分割投資の場合だけ受け入れるべきである
f，g，h に関する解答群
- 表1と変わらない
- 表1に比べて上がる
- 表1に比べて下がる
解答選択欄
- e:
- f:
- g:
- h:
解答
- e=ア
- f=ウ
- g=イ
- h=ウ
解説
〔eについて〕
機能追加後のNPVを表と同じ百万円単位に直し、表1，2のNPVと比較すると下表のようになります。
機能の追加により両案ともにNPVが低下するため、生産課からの要望はどちらの場合も受け入れるべきではないと判断できます。
∴e＝ア：一括投資，分割投資のどちらの場合も受け入れるべきではない
〔f，gについて〕
税引き後効果は、以下の式によって計算されます。
税引き後効果＝コスト削減額－法人税額
法人税額＝(コスト削減額－減価償却費)×法人税率
減価償却費が下がると法人税額が上がるため、結果として税引き後効果は下がることになります。逆に減価償却費が上がれば法人税額が下がるため、税引き後効果は上がります。
したがって減価償却費が下がる2013～2015年の税引き後効果は表1より小さくなり、減価償却費が上がる2016年の税引き後効果は表1より大きくなります。
∴f＝ウ：表1に比べて下がる
g＝イ：表1に比べて上がる
〔hについて〕
現在価値の概念では、同じ金額であっても現在から近い将来に発生するものほど価値が高いと考えます。
減価償却期間を5年にすると投資効果は2013～2015年で現在より減少、2016年で現在より増加します。得られる投資効果の合計は変わりませんが、現在価値の観点で考えると投資効果を得る時期が4年のときより後倒しになってしまっていると捉えることができます。つまり減価償却期間を5年にした場合は、キャッシュを得る時期が遅くなる分だけNPVが減少します。
∴h＝ウ：表1に比べて下がる
機能追加後のNPVを表と同じ百万円単位に直し、表1，2のNPVと比較すると下表のようになります。
∴e＝ア：一括投資，分割投資のどちらの場合も受け入れるべきではない
〔f，gについて〕
税引き後効果は、以下の式によって計算されます。
税引き後効果＝コスト削減額－法人税額
法人税額＝(コスト削減額－減価償却費)×法人税率
減価償却費が下がると法人税額が上がるため、結果として税引き後効果は下がることになります。逆に減価償却費が上がれば法人税額が下がるため、税引き後効果は上がります。
したがって減価償却費が下がる2013～2015年の税引き後効果は表1より小さくなり、減価償却費が上がる2016年の税引き後効果は表1より大きくなります。
∴f＝ウ：表1に比べて下がる
g＝イ：表1に比べて上がる
〔hについて〕
現在価値の概念では、同じ金額であっても現在から近い将来に発生するものほど価値が高いと考えます。
減価償却期間を5年にすると投資効果は2013～2015年で現在より減少、2016年で現在より増加します。得られる投資効果の合計は変わりませんが、現在価値の観点で考えると投資効果を得る時期が4年のときより後倒しになってしまっていると捉えることができます。つまり減価償却期間を5年にした場合は、キャッシュを得る時期が遅くなる分だけNPVが減少します。
∴h＝ウ：表1に比べて下がる